seychellesartprojects.org

Mažiausiai kvadratų regresijos metodo apibrėžimas

Mažiausių kvadratų regresijos metodas yra regresijos analizės forma, nustatanti priklausomo ir nepriklausomo kintamojo santykį kartu su tiesine linija. Ši linija vadinama „geriausiai tinkančia linija“.

Regresijos analizė yra statistinis metodas, kurio pagalba galima įvertinti arba nuspėti nežinomas vieno kintamojo reikšmes iš žinomų kito kintamojo reikšmių. Kintamasis, kuris naudojamas kintamojo palūkanoms numatyti, vadinamas nepriklausomuoju arba aiškinamuoju kintamuoju, o numatomas - kintamuoju.

Panagrinėkime du kintamuosius x & y. Jie braižomi grafike, kurio vertės x yra x ašies vertės y ašyje. Šios vertės pateikiamos taškais žemiau esančiame grafike. Per taškus nubrėžta tiesi linija - vadinama geriausiai tinkančia linija.

Mažiausių kvadratų regresijos tikslas yra užtikrinti, kad per pateiktą reikšmių rinkinį nubrėžta linija nustatytų artimiausią reikšmių ryšį.

Mažiausiai kvadratų regresijos formulė

Regresijos tiesė pagal mažiausių kvadratų metodą apskaičiuojama pagal šią formulę:

ŷ = a + bx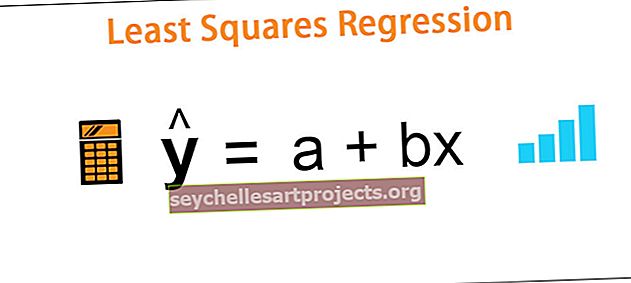

Kur,

• dependent = priklausomas kintamasis
• x = nepriklausomas kintamasis
• a = y-perėmimas
• b = tiesės nuolydis

B tiesės nuolydis apskaičiuojamas pagal šią formulę:

Arba

Y-perėmimas, „a“ apskaičiuojamas pagal šią formulę:

Linija geriausiai tinka mažiausiai kvadrato regresijai

Tinkamiausia linija yra tiesi linija, nubrėžta per taškų sklaidą, geriausiai atspindinti jų tarpusavio santykius.

Panagrinėkime šį grafiką, kuriame duomenų rinkinys nubrėžtas išilgai x ir y ašių. Šie duomenų taškai pavaizduoti naudojant mėlynus taškus. Per šiuos taškus nubrėžtos trys linijos - žalia, raudona ir mėlyna. Žalia linija eina per vieną tašką, o raudona - per tris duomenų taškus. Tačiau mėlyna linija eina per keturis duomenų taškus, o atstumas tarp likusių taškų iki mėlynos linijos yra minimalus, palyginti su kitomis dviem linijomis.

Pirmiau pateiktame grafike mėlyna linija rodo geriausiai tinkančią liniją, nes ji yra arčiausiai visų verčių, o atstumas tarp taškų, esančių už linijos ribų, iki linijos yra minimalus (ty atstumas tarp liekanų ir geriausiai tinkančios linijos - dar vadinamos liekanų kvadratų sumomis). Kitose dviejose linijose - oranžinėje ir žalioje - atstumas tarp liekanų iki linijų yra didesnis, palyginti su mėlyna linija.

Mažiausių kvadratų metodas užtikrina artimiausią ryšį tarp priklausomų ir nepriklausomų kintamųjų, sumažinant atstumą tarp liekanų ir geriausiai tinkančios linijos, ty pagal šį metodą liekanų kvadratų suma yra minimali. Taigi terminas „mažiausiai kvadratai“.

Mažiausiai kvadratų regresijos tiesės pavyzdžiai

Panaudokime šias formules toliau pateiktame klausime -

Šį „Mažiausiai kvadratų regresijos„ Excel “šabloną galite atsisiųsti čia -„ Mažiausiai kvadratų regresijos „Excel“ šablonas “

1 pavyzdys

Išsami informacija apie technikų patirtį įmonėje (per keletą metų) ir jų veiklos įvertinimą pateikta žemiau esančioje lentelėje. Naudodamiesi šiomis vertėmis, įvertinkite techniko, turinčio 20 metų patirtį, darbo įvertinimą.

Sprendimas -

Norėdami pirmiausia apskaičiuoti mažiausius kvadratus, apskaičiuosime Y atkarpą (a) ir tiesės (b) nuolydį taip:

B linijos nuolydis

• b = 6727 - [(80 * 648) / 8] / 1018 - [(80) 2/8]
• = 247/218
• = 1,13

Y perėmimas (a)

• a = 648 - (1,13) (80) / 8
• = 69,7

Regresijos tiesė apskaičiuojama taip:

Formulėje x reikšmė pakeista 20,

• ŷ = a + bx
• ŷ = 69,7 + (1,13) (20)
• ŷ = 92,3

Manoma, kad 20 metų patirtį turinčio techniko darbo įvertinimas yra 92,3.

2 pavyzdys

Mažiausiai kvadratų regresijos lygtis naudojant „Excel“

Mažiausių kvadratų regresijos lygtį galima apskaičiuoti naudojant „Excel“ atlikus šiuos veiksmus:

• Įterpti duomenų lentelę „Excel“.

• Įterpkite sklaidos diagramą naudodami duomenų taškus.

• Įterpkite tendencijų liniją į sklaidos diagramą.

• Pagal tendencijų parinktis pasirinkite linijinę tendencijų liniją ir pasirinkite diagramos rodymo lygtį.

• Mažiausia kvadratų regresijos lygtis tam tikram „Excel“ duomenų rinkiniui rodoma diagramoje.

Taigi apskaičiuojama mažiausio kvadrato regresijos lygtis duotam „Excel“ duomenų rinkiniui. Naudojant lygtį, galima atlikti prognozes ir tendencijų analizę. „Excel“ įrankiai taip pat numato išsamius regresijos skaičiavimus.

Privalumai

• Mažiausių kvadratų regresijos analizės metodas geriausiai tinka prognozavimo modeliams ir tendencijų analizei. Geriausiai jis naudojamas ekonomikos, finansų ir akcijų rinkose, kur bet kokio būsimo kintamojo vertė numatoma naudojant esamus kintamuosius ir jų santykį.
• Mažiausių kvadratų metodas suteikia artimiausią ryšį tarp kintamųjų. Taikant šį metodą, liekanų kvadratų sumų skirtumas iki geriausiai tinkančios linijos yra minimalus.
• Skaičiavimo mechanizmas yra paprastas ir lengvai pritaikomas.

Trūkumai

• Mažiausių kvadratų metodas remiasi nustatant artimiausią ryšį tarp tam tikro kintamųjų rinkinio. Skaičiavimo mechanizmas yra jautrus duomenims, o neįvykusiems (išskirtiniams duomenims) rezultatai paprastai gali turėti didelę įtaką.
• Šis skaičiavimo tipas geriausiai tinka tiesiniams modeliams. Netiesinėms lygtims taikomi išsamesni skaičiavimo mechanizmai.

Išvada

Mažiausių kvadratų metodas yra vienas iš populiariausių metodų, naudojamų prognozavimo modeliams ir tendencijų analizei. Tinkamai apskaičiuojant, gaunami geriausi rezultatai.