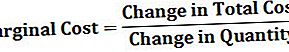Portfelio variacijos formulė (pavyzdys) | Kaip apskaičiuoti portfelio dispersiją?
Kas yra portfelio dispersija?
Sąvoka „portfelio dispersija“ reiškia statistinę šiuolaikinės investicijų teorijos vertę, kuri padeda įvertinti vidutinę portfelio grąžos dispersiją nuo jo vidurkio. Trumpai tariant, tai nustato bendrą portfelio riziką. Ją galima išgauti remiantis svertiniu individualaus dispersijos ir tarpusavio kovariacijos vidurkiu.
Portfelio dispersijos formulė
Matematiškai portfelio dispersijos formulė, susidedanti iš dviejų aktyvų, pateikiama kaip
Portfelio dispersijos formulė = w 1 2 * ơ 1 2 + w 2 2 * ơ 2 2 + 2 * ρ 1,2 * w 1 * w 2 * ơ 1 * ơ 2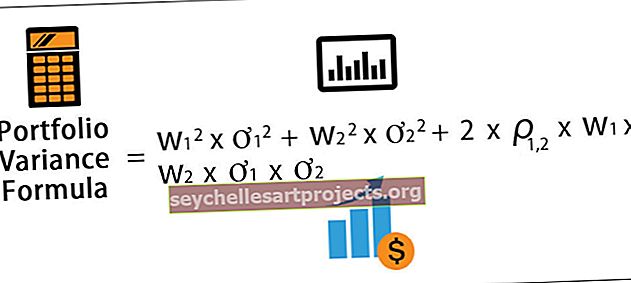
kur,
- w i = turto i portfelio svoris
- ơ i 2 = individualus turto i dispersija
- ρ i, j = i turto ir j turto koreliacija
Vėlgi, dispersija gali būti toliau išplėsta į portfelį, kuriame yra daugiau Nr. turto, pavyzdžiui, 3 turto portfelis gali būti pateiktas kaip
Portfelio dispersijos formulė = w 1 2 * ơ 1 2 + w 2 2 * ơ 2 2 + w 3 2 * ơ 3 2 + 2 * ρ 1,2 * w 1 * w 2 * ơ 1 * ơ 2 + 2 * ρ 2,3 * w 2 * w 3 * ơ 2 * ơ 3 + 2 * ρ 3,1 * w 3 * w 1 * ơ 3* ơ 1
Portfelio dispersijos formulės paaiškinimas
Tam tikro portfelio portfelio dispersijos formulę galima gauti atlikus šiuos veiksmus:
1 žingsnis: Pirma, nustatykite kiekvieno turto svorį visame portfelyje ir jis apskaičiuojamas padalijus turto vertę iš bendros portfelio vertės. I-ojo turto svoris žymimas w i .
2 žingsnis: Tada nustatykite kiekvieno turto standartinį nuokrypį ir jis apskaičiuojamas pagal kiekvieno turto vidutinę ir faktinę grąžą. Standartinis i-ojo turto nuokrypis žymimas ơ i . Standartinio nuokrypio kvadratas yra dispersija, ty ơ i 2.
3 žingsnis: Tada nustatykite turto koreliaciją ir ji iš esmės atspindi kiekvieno turto judėjimą kito turto atžvilgiu. Koreliacija žymima ρ.
4 žingsnis: Galiausiai, dviejų turto portfelio dispersijos formulė nustatoma pagal svertinį individualių dispersijų ir tarpusavio kovariacijos vidurkį, kaip parodyta žemiau.
Portfelio dispersijos formulė = w 1 * ơ 1 2 + w 2 * ơ 2 2 + 2 * ρ 1,2 * w 1 * w 2 * ơ 1 * ơ 2
Portfelio variacijos formulės pavyzdys (su „Excel“ šablonu)
Šį „Portfolio Variance Formula Excel“ šabloną galite atsisiųsti čia - „Portfolio Variance Formula Excel“ šablonas
Paimkime pavyzdį portfelio, kurį sudaro dvi akcijos. A akcijų vertė yra 60 000 USD, o jos standartinis nuokrypis yra 15%, o B atsargų vertė yra 90 000 USD, o jos standartinis nuokrypis yra 10%. Tarp šių dviejų akcijų yra 0,85 koreliacija. Nustatykite dispersiją.
Atsižvelgiant į tai,
- Standartinis A atsargos nuokrypis, ơ A = 15%
- Standartinis B atsargos nuokrypis, ơ B = 10%
Koreliacija, ρ A, B = 0,85
Žemiau yra duomenys, skirti apskaičiuoti dviejų akcijų portfelio dispersiją.

A akcijų svoris, w A = 60 000 USD / (60 000 USD + 90 000 USD) * 100%

Akcijos A svoris = 40% arba 0,40
B akcijų svoris, w B = 90 000 USD / (60 000 USD + 90 000 USD) * 100%

Akcijos B svoris = 60% arba 0,60
Todėl portfelio dispersija bus apskaičiuojama taip,

Dispersija = w A 2 * ơ A 2 + w B 2 * ơ B 2 + 2 * ρ A, B * w A * w B * ơ A * ơ B
= 0,4 ^ 2 * (0,15) 2 + 0,6 ^ 2 * (0,10) 2 + 2 * 0,85 * 0,4 * 0,6 * 0,15 * 0,10

Todėl dispersija yra 1,33%.
Aktualumas ir naudojimas
Vienas ryškiausių portfelio var bruožų yra tai, kad jo vertė nustatoma remiantis kiekvieno turto svertiniu vidurkiu, pakoreguotu jų kovariancijomis. Tai rodo, kad bendrasis dispersija yra mažesnė už paprastą kiekvieno portfelio akcijų individualių svyravimų svertinį vidurkį. Pažymėtina, kad portfelis, kurio vertybiniai popieriai turi mažesnę koreliaciją, turi mažesnį portfelio skirtumą.
Portfelio dispersijos formulės supratimas taip pat yra svarbus, nes tai taikoma šiuolaikinio portfelio teorijoje, kuri remiasi pagrindine prielaida, kad įprasti investuotojai ketina maksimaliai padidinti savo grąžą, kartu sumažinant riziką, pvz., Dispersiją. Investuotojas paprastai siekia vadinamosios efektyvios ribos, ir tai yra žemiausias rizikos ar nepastovumo lygis, kuriuo investuotojas gali pasiekti tikslinę grąžą. Dažniausiai investuotojai investavo į nekoreluotą turtą, kad sumažintų riziką pagal šiuolaikinę portfelio teoriją.
Yra atvejų, kai turtas, kuris gali būti rizikingas atskirai, ilgainiui gali sumažinti portfelio dispersiją, nes tokia investicija greičiausiai padidės, kai sumažės kitos investicijos. Toks sumažėjęs ryšys gali padėti sumažinti hipotetinio portfelio dispersiją. Paprastai portfelio rizikos lygis vertinamas naudojant standartinį nuokrypį, kuris apskaičiuojamas kaip kvadratinė dispersijos šaknis. Tikimasi, kad dispersija išliks didelė, kai duomenų taškai yra toli nuo vidurkio, o tai galiausiai lemia ir aukštesnį bendrą rizikos lygį portfelyje.