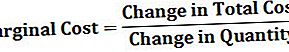seychellesartprojects.org

Formulė populiacijos imties dydžiui nustatyti

Imties dydžio formulė padeda apskaičiuoti arba nustatyti mažiausią imties dydį, kuris reikalingas norint sužinoti tinkamą ar teisingą populiacijos dalį, taip pat patikimumo lygį ir paklaidos ribą.

Terminas „imtis“ reiškia populiacijos dalį, kuri leidžia mums daryti išvadas apie populiaciją, todėl svarbu, kad imties dydis būtų pakankamas, kad būtų galima padaryti reikšmingas išvadas. Kitaip tariant, tai yra minimalus dydis, kurio reikia norint įvertinti tikrąją populiacijos proporciją, naudojant reikiamą klaidų ribą ir pasitikėjimo lygį. Tinkamo imties dydžio nustatymas yra viena iš pasikartojančių statistinės analizės problemų. Jo lygtį galima išgauti naudojant populiacijos dydį, kritinę normalaus pasiskirstymo vertę, imties dalį ir paklaidos ribą.

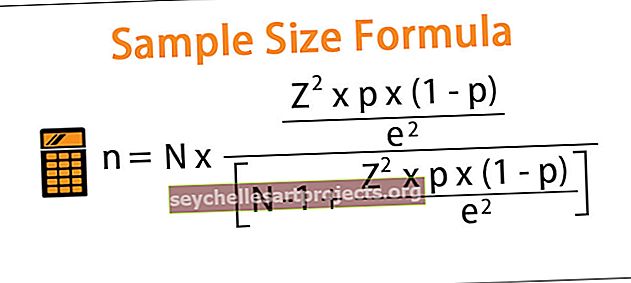
kur,

• N = populiacijos dydis,
• Z = normalaus pasiskirstymo kritinė vertė esant reikalingam patikimumo lygiui,
• p = mėginio dalis,
• e = paklaidos skirtumas

Kaip apskaičiuoti imties dydį? (Žingsnis po žingsnio)

• 1 žingsnis: Pirma, nustatykite populiacijos dydį, kuris yra bendras skirtingų jūsų populiacijos objektų skaičius ir kuris žymimas N. nes imties dydis mažai keičiasi didesnėms nei tai populiacijoms.]
• 2 žingsnis: Tada nustatykite kritinę normalaus pasiskirstymo vertę esant reikalingam patikimumo lygiui. Pavyzdžiui, kritinė vertė esant 95% patikimumo lygiui yra 1,96.
• 3 žingsnis: Tada nustatykite imties dalį, kurią galima naudoti pagal ankstesnių apklausos rezultatus arba surinkti vykdant nedidelę bandomąją apklausą. [Pastaba: jei nesate tikri, visada galite naudoti 0,5 kaip konservatyvų metodą ir tai suteiks didžiausią įmanomą imties dydį.]
• 4 žingsnis: Tada nustatykite klaidos ribą, kuri yra diapazonas, kuriame tikimasi meluoti tikrąją populiaciją . [Pastaba: mažesnė paklaidos riba, tikslumas ir tikslus atsakymas yra daugiau.]
• 5 žingsnis: Galiausiai imties dydžio lygtį galima išgauti naudojant populiacijos dydį (1 žingsnis), kritinę normalaus pasiskirstymo vertę esant reikiamam patikimumo lygiui (2 žingsnis), imties dalį (3 žingsnis) ir paklaidos ribą (žingsnis). 4) kaip parodyta žemiau.

Pavyzdžiai

Šį pavyzdžio dydžio formulės „Excel“ šabloną galite atsisiųsti čia - pavyzdžio dydžio formulės „Excel“ šablonas

1 pavyzdys

Paimkime pavyzdį mažmenininko, kuriam įdomu sužinoti, kiek jų klientų tam tikrą dieną peržiūrėję savo svetainę pirko daiktą iš jų. Atsižvelgiant į tai, kad jų svetainė vidutiniškai per dieną peržiūri 10 000 kartų, nustatykite klientų, kuriuos jie turi stebėti, 95 proc. Patikimumo lygį ir 5 proc.

• Jie nėra tikri dėl dabartinio perskaičiavimo kurso.
• Iš ankstesnių tyrimų jie žino, kad perskaičiavimo koeficientas yra 5%.

Atsižvelgiant į tai,

• Gyventojų skaičius, N = 10 000
• Kritinė vertė esant 95% patikimumo lygiui, Z = 1,96
•  Klaidos skirtumas, e = 5% arba 0,05

1 - Kadangi dabartinis perskaičiavimo kursas nėra žinomas, tarkime, kad p = 0,5

Todėl imties dydį galima apskaičiuoti naudojant tokią formulę:

= (10 000 * (1,96 2) * 0,5 * (1-0,5) / (0,05 2) / (10000 - 1 + ((1,96 2) * 0,5 * (1-0,5) / (0,05 2))))

Todėl 370 klientų pakaks prasmingai daryti išvadą.

2 - Dabartinis perskaičiavimo kursas yra p = 5% arba 0,05

Todėl imties dydį galima apskaičiuoti naudojant pirmiau pateiktą formulę,

= (10 000 * (1,96 2) * 0,05 * (1-0,05) / (0,05 2) / (10000 - 1 + ((1,96 2) * 0,05 * (1-0,05) / (0,05 2))))

Todėl, norint gauti reikšmingą išvadą, šiuo atveju pakaks 72 klientų.

2 pavyzdys

Paimkime aukščiau pateiktą pavyzdį ir šiuo atveju tarkime, kad populiacijos dydis, ty kasdieninis svetainės vaizdas, yra nuo 100 000 iki 120 000, tačiau tiksli vertė nėra žinoma. Likusios vertės yra vienodos kartu su 5% perskaičiavimo rodikliu. Apskaičiuokite 100 000 ir 120 000 imties dydį.

Atsižvelgiant į tai,

• Imties dalis, p = 0,05
• Kritinė vertė esant 95% patikimumo lygiui, Z = 1,96
•  Klaidos skirtumas, e = 0,05

Todėl imties dydį, kai N = 100 000, galima apskaičiuoti taip:

= (100000 * (1,96 2) * 0,05 * (1-0,05) / (0,05 2) / (100000 - 1 + ((1,96 2) * 0,05 * (1-0,05) / (0,05 2))))

Todėl imties dydį, kai N = 120 000, galima apskaičiuoti taip:

= (120000 * (1,96 2) * 0,05 * (1-0,05) / (0,05 2) / (120000 - 1 + ((1,96 2) * 0,05 * (1-0,05) / (0,05 2))))

Todėl įrodyta, kad didėjant populiacijos dydžiui, kuris yra labai didelis, skaičiuojant imties dydį jis tampa nebesvarbus.

Aktualumas ir naudojimas

Imties dydžio apskaičiavimas yra svarbus norint suprasti tinkamo imties dydžio sampratą, nes jis naudojamas tyrimo rezultatams pagrįsti. Jei jis yra per mažas, jis neduos tinkamų rezultatų, o per didelis mėginys gali būti pinigų ir laiko švaistymas. Statistiškai reikšmingas imties dydis daugiausia naudojamas atliekant rinkos tyrimus, sveikatos priežiūros ir švietimo tyrimus.