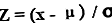seychellesartprojects.org

Formulė Z balui apskaičiuoti

Neapdorotų duomenų Z-balas reiškia balą, gautą matuojant, kiek standartinių nuokrypių yra didesnis arba mažesnis už populiacijos vidurkį, yra duomenys, kurie padeda patikrinti nagrinėjamą hipotezę. Kitaip tariant, tai yra duomenų taško atstumas nuo vidurkio, kuris išreiškiamas kaip standartinio nuokrypio kartotinis.

• Z balai svyruoja nuo -3 karto didesnio nei standartinis nuokrypis (normalaus pasiskirstymo kairėje kairėje) iki +3 karto (standartinio pasiskirstymo dešinėje).
• Z balų vidurkis yra 0, o standartinis nuokrypis yra 1.

Duomenų taško z balo lygtis apskaičiuojama iš duomenų taško atimant populiacijos vidurkį (vadinamą x ), o rezultatas padalijamas iš populiacijos standartinio nuokrypio. Matematiškai jis vaizduojamas kaip

Z balas = (x - μ) / ơ

kur

• x = duomenų taškas
• μ = vidurkis
• ơ = standartinis nuokrypis

Z balo apskaičiavimas (žingsnis po žingsnio)

Duomenų taško z balo lygtį galima nustatyti atlikus šiuos veiksmus:

• 1 žingsnis: Pirma, nustatykite duomenų rinkinio vidurkį, remdamiesi duomenų taškais arba stebėjimais, kurie žymimi x _i , o bendras duomenų taškų skaičius duomenų rinkinyje žymimas N.

• 2 žingsnis: Tada nustatykite populiacijos standartinį nuokrypį, remdamiesi populiacijos vidurkiu μ, duomenų taškais x _i ir duomenų taškų skaičiumi N populiacijoje.

• 3 žingsnis: Galiausiai, z rezultatas gaunamas atimant vidurkį iš duomenų taško, o rezultatas padalijamas iš standartinio nuokrypio, kaip parodyta žemiau.

  

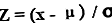
Pavyzdžiai

Šį „Z Score Formula Excel“ šabloną galite atsisiųsti iš čia - „Z Score Formula Excel“ šablonas

1 pavyzdys

Paimkime pavyzdį iš 50 mokinių, kurie praėjusią savaitę parašė gamtos mokslų testą. Šiandien yra rezultatų diena, o klasės auklėtoja pasakojo, kad Jonas testo metu surinko 93 balus, o vidutinis klasės balas buvo 68. Jei standartinis nuokrypis yra 13, nustatykite Johno testo ženklo z balą.

Sprendimas:

Atsižvelgiant į tai,

• Jono testo rezultatas, x = 93
• Vidutinis, μ = 68
• Standartinis nuokrypis, ơ = 13

Todėl Jono testo balo z balą galima apskaičiuoti naudojant aukščiau pateiktą formulę,

Z = (93 - 68) / 13

Z rezultatas bus -

Z rezultatas = 1,92

Todėl Jono „Ztest“ rezultatas yra 1,92 standartinis nuokrypis, viršijantis vidutinį klasės rezultatą, o tai reiškia, kad 97,26% klasės (49 mokiniai) balai buvo mažesni nei Jono.

2 pavyzdys

Paimkime dar vieną išsamų pavyzdį iš 30 mokinių (nes z testas netinka mažiau nei 30 duomenų taškų), kurie pasirodė klasės testui. Nustatykite 4-ojo studento z testo balą pagal mokinių įvertinimus iš 100 - 55, 67, 84, 65, 59, 68, 77, 95, 88, 78, 53, 81, 73, 66 65, 52, 54, 83, 86, 94, 85, 72, 62, 64, 74, 82, 58, 57, 51, 91.

Sprendimas:

Atsižvelgiant į tai,

• x = 65,
• 4-asis studentas surinko = 65,
• Duomenų taškų skaičius, N = 30.

Vidurkis = (55 + 67 + 84 + 65 + 59 + 68 + 77 + 95 + 88 + 78 + 53 + 81 + 73 + 66 + 65 + 52 + 54 + 83 + 86 + 94 + 85 + 72 + 62 + 64 + 74 + 82 + 58 + 57 + 51 + 91) / 30

Vidurkis = 71.30

Dabar standartinį nuokrypį galima apskaičiuoti naudojant toliau pateiktą formulę,

ơ = 13,44

Todėl 4-ojo studento Z-balą galima apskaičiuoti naudojant aukščiau pateiktą formulę,

Z = (x - x) / s

• Z = (65–30) / 13,44
• Z = -0,47

Todėl 4-ojo mokinio balas yra 0,47 standartinis nuokrypis žemesnis už vidutinį klasės balą, o tai reiškia, kad 31,92% klasės (10 mokinių) balų buvo mažiau nei 4-ojo mokinio pagal z-balų lentelę.

Z rezultatas „Excel“ (su „Excel“ šablonu)

Dabar paimkime 2 pavyzdyje minimą atvejį, kad iliustruotume „z-score“ sąvoką žemiau esančiame „Excel“ šablone.

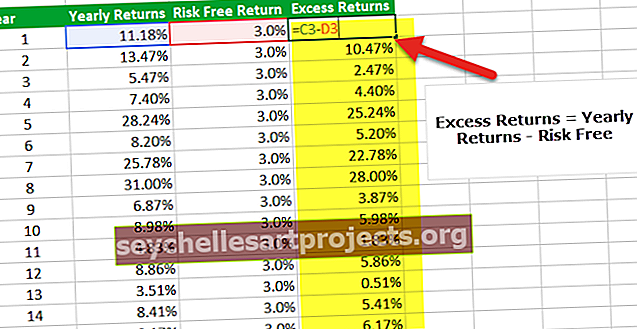
Žemiau pateikiami duomenys, skirti apskaičiuoti Z balą

Norėdami išsamiai apskaičiuoti Z balų formulės bandymų statistiką, galite kreiptis į pateiktą „Excel“ lapą.

Aktualumas ir naudojimas

Žvelgiant iš hipotezių tikrinimo perspektyvos, z-balas yra labai svarbi sąvoka, kurią reikia suprasti, nes ji naudojama norint patikrinti, ar testo statistika patenka į priimtiną vertės diapazoną. Z balas taip pat naudojamas norint standartizuoti duomenis prieš analizę, apskaičiuoti balo tikimybę arba palyginti du ar daugiau duomenų taškų, kurie yra iš skirtingų normalių skirstinių. Tinkamai pritaikius įvairius laukus, „z-score“ taikoma įvairiai.