seychellesartprojects.org

Formulė standartiniam nuokrypiui apskaičiuoti

Mėginio standartinis nuokrypis reiškia statistinę metriką, kuri naudojama norint įvertinti, kiek atsitiktinis kintamasis skiriasi nuo imties vidurkio, ir jis apskaičiuojamas pridedant kiekvieno kintamojo nuokrypio nuo vidurkio kvadratus, tada rezultatą padalijant iš kintamųjų skaičius, atėmus ir paskaičiuojant kvadratinę šaknį pagal rezultatą.

Matematiškai jis vaizduojamas kaip

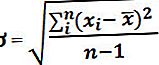
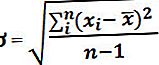
kur

• x _i = atsitiktinis kintamasis
• X = imties vidurkis
• n = kintamųjų skaičius imtyje

Standartinio nuokrypio mėginio apskaičiavimas (žingsnis po žingsnio)

• 1 žingsnis: Pirma, surinkite atsitiktinius kintamuosius iš daugybės kintamųjų populiacijos. Šie kintamieji sudarys imtį. Kintamieji žymimi x _i .
• 2 žingsnis: Tada nustatykite kintamųjų skaičių imtyje ir jis žymimas n.
• 3 žingsnis: Tada nustatykite imties vidurkį, pridėdami visus atsitiktinius kintamuosius ir padaliję rezultatą iš kintamųjų skaičiaus imtyje. Imties vidurkis žymimas x.

• 4 žingsnis: Tada apskaičiuokite skirtumą tarp kiekvieno imties kintamojo ir imties vidurkio, ty x _i - x.
• 5 žingsnis: Tada apskaičiuokite visų nuokrypių kvadratą, ty (x _i - x) 2.
• 6 žingsnis: Tada pridėkite visus nuokrypius iš kvadrato, ty ∑ (x _i - x) 2.
• 7 žingsnis: Tada visų kvadratinių nuokrypių sumą padalykite iš kintamųjų skaičiaus imtyje atėmus vieną, ty (n - 1).
• 8 žingsnis: Galiausiai, imties standartinio nuokrypio formulė apskaičiuojama apskaičiuojant aukščiau paminėto rezultato kvadratinę šaknį, kaip parodyta žemiau.

Pavyzdžiai

Šį standartinio nuokrypio formulės „Excel“ šablono pavyzdį galite atsisiųsti čia - standartinio nuokrypio formulės „Excel“ šablono pavyzdys

1 pavyzdys

Paimkime pavyzdį iš 5 studentų, kurie buvo apklausti, norėdami sužinoti, kiek pieštukų jie naudojo kiekvieną savaitę. Apskaičiuokite standartinį nuokrypį pagal jų pateiktus atsakymus: 3, 2, 5, 6, 4

Atsižvelgiant į tai,

• Imties dydis (n) = 5

Žemiau pateikiami duomenys, skirti apskaičiuoti imties standartinį nuokrypį.

Imties vidurkis

Mėginio vidurkio apskaičiavimas

Imties vidurkis = (3 + 2 + 5 + 6 + 4) / 5

Imties vidurkis = 4

Kiekvieno kintamojo nuokrypių kvadratus galima apskaičiuoti taip, kaip nurodyta toliau,

• (3 - 4) 2 = 1
• (2 - 4) 2 = 4
• (5–4) 2 = 1
• (6 - 4) 2 = 4
• (4 - 4) 2 = 0

Dabar imties standartinį nuokrypį galima apskaičiuoti naudojant aukščiau pateiktą formulę,

• ơ = √ {(1 + 4 + 1 + 4 + 0) / (5 - 1)}

Nukrypimas bus -

• ơ = 1,58

Todėl imties standartinis nuokrypis yra 1,58.

2 pavyzdys

Paimkime biuro Niujorke pavyzdį, kuriame dirba apie 5000 žmonių, ir buvo atlikta 10 žmonių imties apklausa, siekiant nustatyti vidutinį dirbančių gyventojų amžių. Nustatykite standartinį nuokrypį pagal nurodytų 10 žmonių amžių: 23, 27, 33, 28, 21, 24, 36, 32, 29, 25

Atsižvelgiant į tai,

• Imties dydis (n) = 10

Naudodami aukščiau pateiktus duomenis, pirmiausia apskaičiuosime imties vidurkį

Imties vidurkis

Mėginio vidurkio apskaičiavimas

= (23 + 27 + 33 + 28 + 21 + 24 + 36 + 32 + 29 + 25) / 10

Imties vidurkis = 27,8

Kiekvieno kintamojo nuokrypių kvadratus galima apskaičiuoti taip, kaip nurodyta toliau,

• (23 - 27,8) 2 = 23,04
• (27 - 27,8) 2 = 0,64
• (33 - 27,8) 2 = 27,04
• (28 - 27,8) 2 = 0,04
• (21 - 27,8) 2 = 46,24
• (24 - 27,8) 2 = 14,44
• (36 - 27,8) 2 = 67,24
• (32 - 27,8) 2 = 17,64
• (29 - 27,8) 2 = 1,44
• (25 - 27,8) 2 = 7,84

Nukrypimas

Dabar nuokrypį galima apskaičiuoti naudojant aukščiau pateiktą formulę,

• ơ = √ {(23,04 + 0,64 + 27,04 + 0,04 + 46,24 +14,44 +67,24 + 17,64 + 1,44 + 7,84) / (10 - 1)}

Nukrypimas bus -

• ơ = 4,78

Norėdami suprasti išsamų skaičiavimą, galite remtis aukščiau pateiktu „Excel“ lapu.

Aktualumas ir naudojimas

Standartinio nuokrypio imties samprata yra labai svarbi statistikos požiūriu, nes paprastai duomenų imtis imama iš didelių kintamųjų (populiacijos) grupės, iš kurios tikimasi, kad statistikas įvertins arba apibendrins visos populiacijos rezultatus. Standartinio nuokrypio matas nėra išimtis, taigi statistikas turi įvertinti populiacijos standartinį nuokrypį remdamasis imtimi ir būtent tada toks nuokrypis pasireiškia.