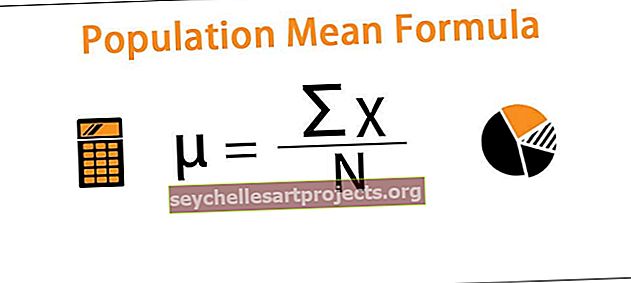seychellesartprojects.org

Formulė imties paklaidai apskaičiuoti

Atrankos klaidos formulė reiškia formulę, kuri naudojama apskaičiuoti statistinę paklaidą, atsirandančią situacijoje, kai testą atliekantis asmuo nepasirenka imties, atspindinčios visą nagrinėjamą populiaciją, ir pagal formulę Atrankos klaida apskaičiuojama dalijant standartinis populiacijos nuokrypis iš imties dydžio kvadratinės šaknies ir gautas rezultatas padauginamas iš Z balo vertės, pagrįstos patikimumo intervalu.

Imties klaida = Z x (σ / √ n)

Kur,

• Z yra Z balo vertė, pagrįsta pasitikėjimo intervalu
• σ yra populiacijos standartinis nuokrypis
• n yra imties dydis

Žingsnis po žingsnio imties klaidos apskaičiavimas

• 1 veiksmas : surinko visus duomenis, vadinamus gyventojais. Apskaičiuokite populiacijos vidurkį ir populiacijos standartinį nuokrypį.
• 2 žingsnis : Dabar reikia nustatyti imties dydį, be to, imties dydis turi būti mažesnis nei populiacija ir jis neturėtų būti didesnis.
• 3 žingsnis : nustatykite patikimumo lygį ir atitinkamai pagal jo lentelę galite nustatyti Z balo vertę.
• 4 žingsnis : Dabar padauginkite Z balą iš populiacijos standartinio nuokrypio ir padalykite jį iš imties dydžio kvadratinės šaknies, kad gautumėte klaidos ribą arba imties dydžio paklaidą.

Pavyzdžiai

Čia galite atsisiųsti šį pavyzdžio klaidos formulės „Excel“ šabloną - „Excel“ šablono pavyzdžių klaidų formulė

1 pavyzdys

Tarkime, kad populiacijos standartinis nuokrypis yra 0,30, o imties dydis - 100. Kokia bus atrankos paklaida esant 95% patikimumo lygiui?

Sprendimas

Čia mums pateikiamas populiacijos standartinis nuokrypis ir imties dydis, todėl tam pačiam apskaičiuoti galime naudoti žemiau pateiktą formulę.

Skaičiavimui naudokite šiuos duomenis.

Todėl imties paklaida apskaičiuojama taip:

Atrankos klaida bus -

2 pavyzdys

Šiuo metu Gautamas tęsia buhalterijos kursą ir išlaiko stojamąjį egzaminą. Dabar jis užsiregistravo į vidurinį lygį ir taip pat eis į vyresniojo buhalterio praktiką. Jis dirbs atlikdamas gamybos įmonių auditą. 

Vienos iš firmų, kuriose jis lankėsi pirmą kartą, buvo paprašyta patikrinti, ar visų pirkimų įrašų sąskaitos yra pagrįstai prieinamos. Jo pasirinktas imties dydis buvo 50, o populiacijos standartinis nuokrypis buvo 0,50.

Remiantis turima informacija, turite apskaičiuoti atrankos paklaidą esant 95% ir 99% patikimumo intervalui.

Sprendimas

Čia mums pateikiamas populiacijos standartinis nuokrypis ir imties dydis, todėl tam pačiam apskaičiuoti galime naudoti žemiau pateiktą formulę.

Z rezultatas 95% patikimumo lygiui bus 1,96 (galima rasti Z balų lentelėje)

Skaičiavimui naudokite šiuos duomenis.

Todėl apskaičiuojama taip,

Atrankos klaida bus -

Z rezultatas 95% patikimumo lygiui bus 2,58 (galima rasti Z balų lentelėje)

Skaičiavimui naudokite šiuos duomenis.

Todėl apskaičiuojama taip,

Atrankos klaida bus -

Didėjant patikimumo lygiui, didėja ir atrankos paklaida.

3 pavyzdys

Mokykloje buvo organizuojamas biometrinis užsiėmimas, siekiant patikrinti mokinių sveikatą. Užsiėmimas buvo pradėtas kartu su X klasės mokiniais. Iš viso B skyriuje yra 30 studentų. Tarp jų 12 studentų buvo atsitiktinai atrinkti atlikti išsamią patikrą ir poilsį. Buvo atliktas vienintelis pagrindinis testas. Ataskaitoje daroma išvada, kad vidutinis B skyriaus mokinių ūgis yra 154.

Sprendimas

Populiacijos standartinis nuokrypis buvo 9,39. Remiantis aukščiau pateikta informacija, turite apskaičiuoti 90% ir 95% patikimumo intervalų atrankos paklaidą.

Čia mums pateikiamas populiacijos standartinis nuokrypis ir imties dydis, todėl mes galime naudoti žemiau pateiktą formulę tam pačiam apskaičiuoti.

Z rezultatas 95% patikimumo lygiui bus 1,96 (galima rasti Z balų lentelėje)

Skaičiavimui naudokite šiuos duomenis.

Todėl imties paklaida apskaičiuojama taip:

Atrankos klaida bus -

90% patikimumo lygio Z rezultatas bus 1,645 (galima gauti iš „Z“ balų lentelės)

Skaičiavimui naudokite šiuos duomenis.

Todėl apskaičiuojama taip,

Atrankos klaida bus -

Mažėjant patikimumo lygiui, mažėja ir atrankos paklaida.

Aktualumas ir naudojimas

Tai labai svarbu norint suprasti šią koncepciją, nes tai parodys, kiek galima tikėtis, kad tyrimo rezultatai iš tikrųjų atspindės faktinį gyventojų požiūrį. Reikia nepamiršti vieno dalyko, kad apklausa atliekama naudojant mažesnę populiaciją, vadinamą imties dydžiu (taip pat kitaip vadinamą apklausos respondentais), kad atstovautų didesnei populiacijai.

Tai gali būti vertinama kaip tyrimo efektyvumo apskaičiavimo būdas. Kai atrankos skirtumas yra didesnis, tai rodo, kad tyrimo pasekmės gali nukrypti nuo faktinio bendro gyventojų skaičiaus. Kita vertus, imties paklaida arba paklaidos riba yra mažesnė, nei tai rodo, kad pasekmės dabar yra artimesnės tikrajam visų gyventojų skaičiui ir tai padidins pasitikėjimą nagrinėjamu tyrimu.