seychellesartprojects.org

Gyventojų vidurkio apskaičiavimo formulė

Populiacijos vidurkis yra visų nurodytos populiacijos reikšmių vidurkis arba vidurkis ir apskaičiuojamas susumavus visas populiacijos reikšmes, žymimas X susumavus, padalijus iš populiacijos reikšmių skaičiaus, kuris žymimas N.

Jis gaunamas susumavus visus stebėjimus grupėje ir suskaidžius sumą iš stebėjimų skaičiaus. Kai statistinių parametrų skaičiavimui imamas visas duomenų rinkinys, duomenų rinkinys yra visuma. Pavyzdžiui, visų NASDAQ vertybinių popierių biržoje kotiruojamų akcijų grąža tos grupės gyventojams. Šiame pavyzdyje visų NASDAQ biržoje kotiruojamų akcijų grąžos vidurkis bus visų toje biržoje išvardytų akcijų grąžos vidurkis.

Norėdami apskaičiuoti grupės populiacijos vidurkį, pirmiausia turime išsiaiškinti visų stebėtų verčių sumą. Taigi, jei bendras pastebėtų verčių skaičius žymimas X, visų stebimų verčių suma bus ∑X. Tegul stebėjimų skaičius populiacijoje yra N.

Formulė pateikiama taip,

µ = ∑X / N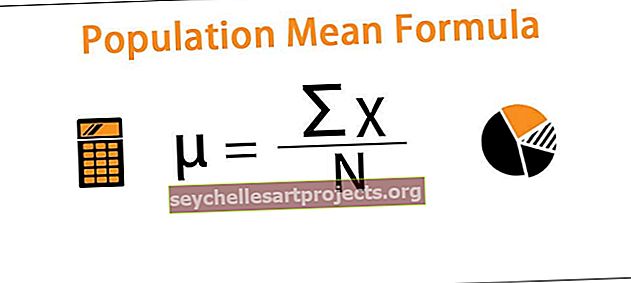

• µ = populiacijos vidurkis

Pavyzdžiai

Galite atsisiųsti šį „Excel“ vidutinės formulės „Excel“ šabloną iš čia - „Population Mean Formula Excel“ šablonas

1 pavyzdys

Pabandykime išanalizuoti atsargų XYZ grąžą per pastaruosius dvylika metų. Per pastaruosius dvylika metų akcijų grąža yra 12%, 25%, 16%, 14%, 40%, 15%, 13%, 17%, 23%, 13%, 17% ir 19%. Norėdami apskaičiuoti visos populiacijos vidurkį, pirmiausia turime išsiaiškinti visų pastebėtų verčių sumą. Taigi šiame pavyzdyje ∑X yra 224%, o pastebėtų populiacijos verčių skaičius yra 12, nes tai apima atsargų grąžą 12 metų laikotarpiui.

Naudodami šiuos du kintamuosius, pagal formulę galime apskaičiuoti atsargų grąžos vidurkį.

Toliau pateikiami pateikti duomenys

Todėl naudojant aukščiau pateiktą informaciją, vidurkį galima apskaičiuoti kaip

• µ = 224% / 12

Pavyzdys rodo, kad vidutinė arba vidutinė stebėtos vertės grąža yra 19%. 

2 pavyzdys

Pabandykime išanalizuoti teminio savitarpio fondo grąžą per pastaruosius aštuonerius metus. Per pastaruosius dvylika metų akcijų grąža yra 25%, 16%, 14%, 15%, 13%, 23%, 33% ir 27%. Norėdami apskaičiuoti visos populiacijos vidurkį, pirmiausia turime išsiaiškinti visų pastebėtų verčių sumą. Taigi šiame pavyzdyje ∑X yra 166%, o gyventojų stebimų verčių skaičius yra 8, nes tai apima investicinio fondo grąžą 8 metams.

Naudodami šiuos du kintamuosius, pagal formulę galime apskaičiuoti atsargų grąžos vidurkį.

Žemiau pateikiami skaičiavimo duomenys

Todėl vidurkį galima apskaičiuoti kaip

• µ = 166% / 8

Pavyzdys rodo, kad vidutinė arba vidutinė stebėtos vertės grąža yra 21%. 

3 pavyzdys

Išsiaiškinkime 15 mokinių svorio populiacijos vidurkį klasėje. Kiekvieno 15 mokinių klasės mokinio svoris kg yra toks: 35, 36, 42, 40, 44, 45, 38, 42, 39, 42, 44, 45, 48, 42 ir 40. Siekiant apskaičiuokite visos populiacijos vidurkį, pirmiausia turime išsiaiškinti visų pastebėtų verčių sumą. Taigi šiame pavyzdyje ∑X yra 622 Kg, o pastebėtų populiacijos verčių skaičius yra 15, nes jis apima 15 studentų svorį.

Naudodami šiuos du kintamuosius, pagal formulę galime apskaičiuoti atsargų grąžos vidurkį.

Toliau pateikiami pateikti skaičiavimo duomenys

Todėl naudojant aukščiau pateiktą informaciją populiacijos vidurkį galima apskaičiuoti kaip

• µ = 622/15

 Pavyzdys rodo, kad vidutinė arba vidutinė stebėtos vertės grąža yra 41,47

Aktualumas ir naudojimas

Populiacijos vidurkis yra labai svarbus statistinis parametras. Tai padeda žinoti gyventojų parametrų vidurkį. Vidurkis yra svarbus, nes jis naudojamas apskaičiuojant kelis kitus statistinius parametrus, pvz., Dispersiją, standartinius nuokrypius ir kitus. Jis apskaičiuojamas pagal aritmetinio vidurkio formulės sampratą ir nurodo vidurkį ar vidurkį, pagal kurį galima daryti išvadą, ar stebėjimas yra didelis, ar žemas visoje stebėjimų populiacijoje.