seychellesartprojects.org

Statistikoje turime terminą, vadinamą lognormaliniu pasiskirstymu, kuris apskaičiuojamas norint sužinoti kintamojo, kurio logaritmas yra normaliai pasiskirstęs, pasiskirstymą. Originali formulė yra labai sudėtinga formulė jai apskaičiuoti, tačiau „Excel“ sistemoje turime integruotą funkciją apskaičiuoti lognormalą paskirstymas kuris Lognorm.Dist funkcija.

Kas yra „Lognormal Distribution“ programoje „Excel“

Normalus logaritminis skirstinys pateikia nuolatinį atsitiktinio kintamojo statistinį pasiskirstymą, kuris paprastai paskirstomas logaritmu. Toliau pateikiami lognormalių funkcijų, naudojamų „Excel“ tipai:

LOGNORM.DIST formulė

Pasiskirstymo funkcijos sintaksė yra apibrėžiama kaip LOGNORM.DIST (x, vidurkis, standartinis nuokrypis, kaupiamasis) Excel, kuris pateikia lognormalų x pasiskirstymą su nurodytais natūralaus logaritmo Ln (x) vidurkio ir standartinio nuokrypio parametrais. Pirmiau minėta funkcija reikalauja šių parametrų ar argumentų: -

• x: - reikalaujama „x“ vertė, kurios logistinis pasiskirstymas turi būti grąžintas.
• vidurkis: - Ln (x) vidurkis
• standartinis nuokrypis: - standartinis Ln (x) nuokrypis
• kaupiamasis: - Jei kaupiamasis yra TIESA, funkcija grąžina kaupiamąjį pasiskirstymą, kitaip FALSE pateikia tikimybės tankį.

Kaupiamojo pasiskirstymo funkcija (CDF) yra tikimybės kintamasis, kurio vertė yra mažesnė nei lygi x. Nuolatinio atsitiktinio kintamojo tikimybės tankio funkcija (PDF) paaiškina santykinę atsitiktinio kintamojo x tikimybę įgyti tam tikrą vertę.

LOGNORM.DIST taip pat yra naudingas analizuojant akcijų kainas, nes apskaičiuojant akcijų kainą negalima taikyti įprasto pasiskirstymo. Funkcija taip pat gali būti naudojama apskaičiuojant „Black Scholes“ modelio pasirinkimo kainą.

„Lognormal Distribution Excel“ parametrų skaičiavimas

Panagrinėkime keletą „lognormal“ pasiskirstymo pavyzdžių, naudojamų „Excel“.

Šį „Lognormal Distribution Excel“ šabloną galite atsisiųsti čia - „Lognormal Distribution Excel“ šablonas

Apsvarstykite žemiau kotiruojamų bendrovių akcijų kainą, kad gautumėte vidutinius ir standartinius nuokrypio „Excel“ parametrus.

1 žingsnis: - Dabar apskaičiuokite natūralių logaritmų vertes atitinkamoms akcijų kainoms.

Kaip matyti iš pirmiau pateiktų duomenų, = LN (skaičius) grąžina nurodyto skaičiaus natūraliojo logaritmo vertę.

2 žingsnis: - Tada apskaičiuokite natūralaus logaritmo skaičių kvadratas, tas pats parodyta žemiau esančioje lentelėje.

3 žingsnis: - Norint apskaičiuoti standartinį nuokrypį, dabar mums taip pat reikės akcijų kainos natūralaus logaritmo ir kvadratinių natūralių logaritmų verčių sumos.

4 žingsnis: - Tada apskaičiuokite akcijų kainos natūralaus logaritmo vidurkį.

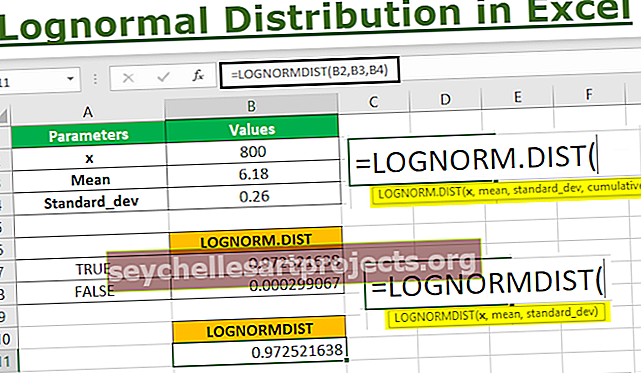
Vidurkis, µ = (5,97 + 5,99 + 6,21 + 6,54) / 4

Arba µ = 6.18

5 žingsnis: - Standartinio nuokrypio apskaičiavimas gali būti atliekamas rankiniu būdu ir naudojant tiesioginę „Excel“ formulę.

Žemiau pateikiama akcijų kainos vidurkio ir standartinio nuokrypio verčių lentelė.

Standartinis nuokrypis apskaičiuojamas naudojant = STDEV.S (natūralaus logaritmo stulpelio diapazonas ln (atsargų kaina)).

Tačiau pirmiau minėti vidutinio ir standartinio nuokrypio parametrai gali būti toliau naudojami apskaičiuojant bet kurios nurodytos vertės „X“ arba akcijų kainos Excel lognormalų pasiskirstymą. To paties paaiškinimas parodytas žemiau.

1 veiksmas: - Apsvarstykite toliau pateiktą lentelę, kad suprastumėte funkciją LOGNORM.DIST

Aukščiau pateiktoje lentelėje pateikiamos parametrų vertės, reikalingos apskaičiuoti „Excel“ lognormalųjį x pasiskirstymą, kuris yra 10.

2 žingsnis: - Dabar, norėdami gauti rezultatą, į formulės funkciją įterpsime reikšmes, pasirinkdami argumentus B2, B3, B4, o kaupiamasis parametras turės parinktis TRUE ir FALSE.

LOGNORM.DIST (x, vidurkis, standartinis nuokrypis, kaupiamasis)

Kaip parodyta pirmiau pateiktoje ekrano kopijoje, pirmiausia įveskite parinktį TRUE, kad gautumėte kaupiamojo paskirstymo funkciją.

Tokiu būdu gauname vertę, kaip parodyta ląstelėje C19 kaupiamojo pasiskirstymo funkcijai (CDF).

3 žingsnis: - Dabar apskaičiuokime tikimybės tankio funkcijos (PDF) lognormalų pasiskirstymą „Excel“, kaupiamajame parametre pasirinkdami tą patį argumentą B2, B3, B4 ir FALSE.

Kaip matyti aukščiau pateiktame paveikslėlyje, gauname rezultatą tikimybės tankio funkcijos (PDF) ląstelėje C20.

4 žingsnis: - Kaip matyti iš pirmiau nurodytos funkcijos, LOGNORM.DIST yra suderinamas su 2010 m. „Excel“ ir vėlesnėmis versijomis. Tačiau mes taip pat galime naudoti LOGNORMDIST, kuris naudoja tuos pačius parametrus kaip ir naujausiose versijose. Atsižvelgdami į tas pačias parametrų reikšmes, užpildysime LOGNORMDIST funkciją, kaip parodyta žemiau.

Kaip matyti, vertės rezultatas buvo tas pats, kaip kaupiamojo argumento TRUE parametro reikšmė LOGNORM.DIST.

Įsimintini dalykai apie „Normal Loglog“ paskirstymą „Excel“

1. Jei kuris nors parametras ar argumentas nėra skaitinis, lognormalusis skirstinys išsiskiria funkcija grąžins #VALUE! klaidos pranešimas.
2. Jei argumentai x yra mažesni ir lygūs 0 arba jei standartinis nuokrypis yra mažesnis ir lygus 0, funkcija grąžins #NUM! klaidos pranešimas.
3. LOGNORM.DIST apskaičiuoti ekvivalentinė išraiška yra LOGNORM.DIST (x, vidurkis, standartinis_nukrypimas) = ​​NORM.S.DIST ((ln (x) -medžiaga) / standartinis_dev)
4. Ši funkcija yra suderinama su 2010 m. Ir vėlesnėmis versijomis. 2007 m. Ir ankstesnėse versijose turi būti naudojama „LOGNORMDIST“ (x, vidurkis, standartinis_įrenginys), kuri pateikia kaupiamąjį lognormalų x skirstinį, kur ln (x) paprastai paskirstomas su parametrais / argumentais „mean“ standartinis nuokrypis.