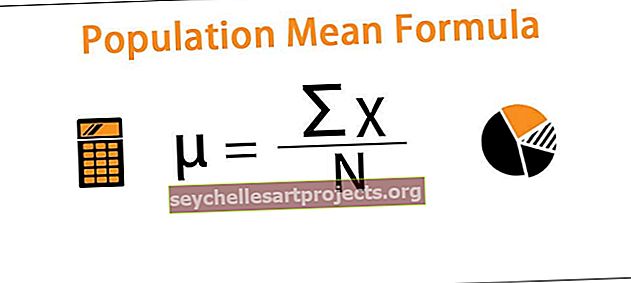Gyventojų dispersijos formulė Žingsnis po žingsnio skaičiavimas | Pavyzdžiai
Populiacijos dispersijos apskaičiavimo formulė
Populiacijos dispersijos formulė yra vidutinių populiacijos duomenų atstumų matas. Ji apskaičiuojama apskaičiuojant populiacijos formulės vidurkį, o dispersija apskaičiuojama pagal kintamųjų kvadrato sumą atėmus vidurkį, padalytą iš daugybės populiacijos stebėjimų.
Populiacijos dispersija yra populiacijos duomenų plitimo matas. Taigi populiacijos dispersiją galima apibrėžti kaip atstumų nuo kiekvieno duomenų taško tam tikroje populiacijoje iki vidurkio, kvadrato, vidurkį, ir tai rodo, kaip duomenų taškai yra pasiskirstę populiacijoje. Gyventojų dispersija yra svarbus statistikoje naudojamas sklaidos matas. Statistikai apskaičiuoja dispersiją, norėdami nustatyti, kaip atskiri duomenų rinkinio skaičiai yra susiję vienas su kitu.
Skaičiuojant populiacijos dispersiją, dispersija apskaičiuojama atsižvelgiant į populiacijos vidurkį. Taigi, norėdami apskaičiuoti populiacijos dispersiją, turime išsiaiškinti populiacijos vidurkį. Vienas populiariausių pranešimų apie gyventojų dispersiją yra σ2. Tai tariama kaip sigmos kvadratas.
Populiacijos dispersiją galima apskaičiuoti naudojant šią formulę:


kur
- σ2 yra populiacijos dispersija,
- x 1, x 2 , x 3, ... ..x n yra stebėjimai
- N yra stebėjimų skaičius,
- µ yra duomenų rinkinio vidurkis
Žingsnis po žingsnio gyventojų dispersijos apskaičiavimas
Populiacijos dispersijos formulę galima apskaičiuoti atlikus šiuos penkis paprastus veiksmus:
- 1 žingsnis: Apskaičiuokite pateiktų duomenų vidurkį (µ). Norėdami apskaičiuoti vidurkį, pridėkite visus stebėjimus ir padalykite tai iš stebėjimų skaičiaus (N).
- 2 žingsnis: Padarykite lentelę. Atkreipkite dėmesį, kad lentelės sukūrimas nėra privalomas, tačiau pateikiant jį lentelių pavidalu, būtų lengviau atlikti skaičiavimus. Pirmame stulpelyje užrašykite kiekvieną stebėjimą (x 1, x 2 , x 3, ... ..x n ).
- 3 žingsnis: Antrame stulpelyje užrašykite kiekvieno stebėjimo nuokrypį nuo vidurkio (x i - µ).
- 4 žingsnis: Trečiame stulpelyje užrašykite kiekvieno stebėjimo kvadratą iš vidurkio (x i - µ) 2. Kitaip tariant, kvadratuokite kiekvieną iš 2 stulpelyje gautų skaičių.
- 5 žingsnis: Vėliau turime pridėti trečiajame stulpelyje gautus skaičius. Raskite kvadratų nuokrypių sumą ir padalykite taip gautą sumą iš stebėjimų skaičiaus (N). Tai padės mums
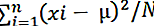 išsiaiškinti populiacijos skirtumus.
išsiaiškinti populiacijos skirtumus.
Pavyzdžiai
Šį „Population Variance Formula Excel“ šabloną galite atsisiųsti iš čia - „Population Variance Formula Excel“ šablonas1 pavyzdys
Apskaičiuokite populiacijos dispersiją iš šių 5 stebėjimų: 50, 55, 45, 60, 40.
Sprendimas:
Norėdami apskaičiuoti populiacijos dispersiją, naudokite šiuos duomenis.

Iš viso yra 5 stebėjimai. Vadinasi, N = 5.
µ = (50 + 55 + 45 + 60 + 40) / 5 = 250/5 = 50
Taigi, populiacijos dispersijos σ2 apskaičiavimą galima atlikti taip:


σ2 = 250/5
Gyventojų dispersija σ2 bus

Populiacijos dispersija (σ2) = 50
Populiacijos dispersija yra 50.
2 pavyzdys
„XYZ Ltd.“ yra maža įmonė, kurią sudaro tik 6 darbuotojai. Generalinis direktorius mano, kad šių darbuotojų atlyginimai neturėtų būti labai nevienodi. Šiuo tikslu jis nori, kad jūs apskaičiuotumėte šių atlyginimų dispersiją. Šių darbuotojų atlyginimai yra tokie, kokie yra. Apskaičiuokite generalinio direktoriaus atlyginimų gyventojų dispersiją.
Sprendimas:
Norėdami apskaičiuoti populiacijos dispersiją, naudokite šiuos duomenis.

Iš viso yra 6 stebėjimai. Taigi, N = 6.
= (30 + 27 + 20 + 40 + 32 + 31) / 6 = 180/6 = 30 USD
Taigi, populiacijos dispersijos σ2 apskaičiavimą galima atlikti taip:


σ2 = 214/6
Gyventojų dispersija σ2 bus

Populiacijos dispersija (σ2) = 35,67
Gyventojų algų dispersija yra 35,67.
3 pavyzdys
„Sweet Juice Ltd“ gamina įvairių skonių sultis. Valdymo departamentas perka 7 didelius konteinerius šioms sultims laikyti gamykloje. Kokybės kontrolės departamentas nusprendė, kad konteinerius atmes, jei konteinerių dispersija viršija 10. Pateikti 7 konteinerių svoriai kg: 105, 100, 102, 95, 100, 98 ir 107. Prašome patarti kokybės Kontrolės departamentas, ar jis turėtų atmesti konteinerius.
Sprendimas:
Norėdami apskaičiuoti populiacijos dispersiją, naudokite šiuos duomenis.

Iš viso yra 7 stebėjimai. Vadinasi, N = 7
= (105 + 100 + 102 + 95 + 100 + 98 + 107) / 7 = 707/7 = 10
Taigi, populiacijos dispersijos σ2 apskaičiavimą galima atlikti taip:


σ2 = 100/7
Gyventojų dispersija σ2 bus

Populiacijos dispersija (σ2) = 14,29
Kadangi dispersija (14,29) viršija 10 ribą, kurią nusprendė kokybės kontrolės departamentas, konteinerius reikėtų atmesti.
4 pavyzdys
Ligoninės, pavadintos „Sagar Healthcare“, valdymo komanda užfiksavo, kad pirmąją 2019 m. Kovo savaitę gimė 8 kūdikiai. Gydytojas norėjo įvertinti kūdikių sveikatą ir aukščio dispersiją. Šių kūdikių ūgis yra toks: 48 cm, 47 cm, 50 cm, 53 cm, 50 cm, 52 cm, 51 cm, 60 cm. Apskaičiuokite šių 8 kūdikių ūgio dispersiją.
Sprendimas:
Norėdami apskaičiuoti populiacijos dispersiją, naudokite šiuos duomenis.

Taigi, populiacijos dispersijos σ2 apskaičiavimą galima atlikti taip:

„Excel“ yra integruota populiacijos dispersijos formulė, kurią galima naudoti skaičiuojant skaičių grupės populiacijos dispersiją. Pasirinkite tuščią langelį ir įveskite šią formulę = VAR.P (B2: B9). Čia B2: B9 yra langelių diapazonas, pagal kurį norite apskaičiuoti populiacijos dispersiją.
Gyventojų dispersija σ2 bus

Populiacijos dispersija (σ2) = 13,98
Aktualumas ir naudojimas
Populiacijos dispersija naudojama kaip sklaidos matas. Panagrinėkime dvi populiacijos grupes, kurių stebėjimų vidurkis ir skaičius yra vienodi. 1 duomenų rinkinį sudaro 5 skaičiai - 55, 50, 45, 50 ir 50. 2 duomenų rinkinį sudaro 10, 50, 85, 90 ir 15. Abiejų duomenų rinkinių vidurkis yra tas pats, kuris yra 50. Bet, 1 duomenų rinkinyje reikšmės yra arti viena kitos, o 2 duomenų rinkinyje yra išsklaidytos vertės. Dispersija suteikia mokslinį šio artumo / sklaidos matą. 1 duomenų rinkinio dispersija yra tik 10, o 2 duomenų rinkinyje - 1130. Taigi didelis dispersija rodo, kad skaičiai yra toli nuo vidurkio ir vienas nuo kito. Mažas dispersija rodo, kad skaičiai yra arti vienas kito.
Variacijos naudojamos portfelio valdymo srityje vykdant turto paskirstymą. Investuotojai apskaičiuoja turto grąžos dispersiją, kad nustatytų optimalius portfelius, optimizuodami du pagrindinius parametrus - grąžą ir nepastovumą. Nepastovumas, matuojamas dispersija, yra konkretaus finansinio užtikrinimo rizikos matas.

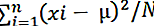 išsiaiškinti populiacijos skirtumus.
išsiaiškinti populiacijos skirtumus.