Z bandymo formulė statistikoje Žingsnis po žingsnio skaičiavimas (pavyzdžiai)

Formulė Z testui apskaičiuoti statistikoje

Z Statistikos testas reiškia hipotezės testą, kuris naudojamas norint nustatyti, ar skiriasi dviejų apskaičiuotų imčių vidurkiai, jei yra standartiniai nuokrypiai ir imtis yra didelė.

Z = (x - μ) / ơ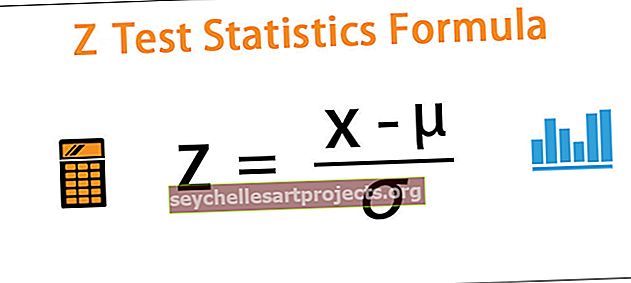

kur x = bet kuri populiacijos vertė

μ = populiacijos vidurkis
population = populiacijos standartinis nuokrypis

Imties atveju z bandymo vertės statistikos formulė apskaičiuojama iš x vertės atėmus imties vidurkį, o rezultatas padalijamas iš imties standartinio nuokrypio. Matematiškai jis vaizduojamas kaip

Z = (x - x_ reikšmė ) / s

kur

x = bet kuri imties reikšmė
x_mean = imties vidurkis
s = imties standartinis nuokrypis

Z bandymo skaičiavimas (žingsnis po žingsnio)

Populiacijos z testo statistikos formulė gaunama atlikus šiuos veiksmus:

1 žingsnis: Pirma, apskaičiuokite populiacijos vidurkį ir populiacijos standartinį nuokrypį, remdamiesi stebėjimu, užfiksuotu populiacijos vidurkyje, ir kiekvienas stebėjimas žymimas x _i . Bendras populiacijos stebėjimų skaičius žymimas N.

Gyventojų vidurkis,

Populiacijos standartinis nuokrypis,

2 žingsnis: Galiausiai, z testo statistika apskaičiuojama iš kintamojo atėmus populiacijos vidurkį, o rezultatas padalijamas iš populiacijos standartinio nuokrypio, kaip parodyta žemiau.

Z = (x - μ) / ơ

Imties z testo statistikos formulė gaunama atlikus šiuos veiksmus:

1 žingsnis: Pirmiausia apskaičiuokite imties vidurkį ir imties standartinį nuokrypį, kaip nurodyta aukščiau. Čia bendras stebėjimų skaičius imtyje žymimas n tokiu, kad n <N.

Imties vidurkis,

Mėginio standartinis nuokrypis,

2 žingsnis: Galiausiai, z testo statistika apskaičiuojama iš x vertės atėmus imties vidurkį, o rezultatas padalijamas iš imties standartinio nuokrypio, kaip parodyta žemiau.

Z = (x - x_ reikšmė ) / s

Pavyzdžiai

Šį „Z Test Formula Excel“ šabloną galite atsisiųsti čia - „Z Test Formula Excel“ šablonas

1 pavyzdys

Tarkime, kad mokykloje atsirado mokinių, kurie pasirodė klasės testui. Vidutinis testo balas yra 75, o standartinis nuokrypis yra 15. Nustatykite Davidui, kuris teste surinko 90 balų, z-testo balą.

Atsižvelgiant į tai,

Populiacijos vidurkis, μ = 75
Populiacijos standartinis nuokrypis, ơ = 15

Todėl z testo statistiką galima apskaičiuoti kaip:

Z = (90–75) / 15

Z bandymų statistika bus -

Z = 1

Todėl Dovydo testo rezultatas yra vienas standartinis nuokrypis, viršijantis vidutinį gyventojų balą, ty pagal z balų lentelę 84,13% studentų gavo mažiau balų nei Deividas.

2 pavyzdys

Paimkime pavyzdį iš 30 studentų, kurie buvo atrinkti kaip apklausos pavyzdinės komandos dalis, kad pamatytume, kiek pieštukų buvo naudojama per savaitę. Pagal pateiktus atsakymus nustatykite 3-ojo studento z testo balą: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7.

Atsižvelgiant į tai,

x = 5, nes 3-iojo mokinio atsakymas yra 5
Imties dydis, n = 30

Imties vidurkis, = (3 + 2 + 5 + 6 + 4 + 7 + 4 + 3 + 3 + 8 + 3 + 1 + 3 + 6 + 5 + 2 + 4 + 3 + 6 + 4 + 5 + 2 + 2 + 4 + 4 + 2 + 8 + 3 + 6 + 7) / 30

Vidurkis = 4,17

Dabar imties standartinį nuokrypį galima apskaičiuoti naudojant aukščiau pateiktą formulę.

ơ = 1,90

Todėl 3-ojo studento z testo balą galima apskaičiuoti taip:

Z = (x - x) / s

Z = (5–17) / 1,90
Z = 0,44

Todėl 3-iojo studento naudojimas yra 0,44 karto didesnis už standartinį nuokrypį, viršijantį vidutinį imties naudojimą, ty pagal z-balų lentelę 67% studentų naudoja mažiau pieštukų nei 3-asis studentas.

3 pavyzdys

Žemiau pateikiami duomenys Z bandymo statistikai apskaičiuoti

Norėdami išsamiai apskaičiuoti Z bandymų statistiką, galite kreiptis į pateiktą „Excel“ lapą.

Aktualumas ir naudojimas

Labai svarbu suprasti „z-test“ statistikos sąvoką, nes ji paprastai naudojama visada, kai galima ginčytis, ar testo statistika atitinka normalų pasiskirstymą pagal atitinkamą nulinę hipotezę. Tačiau reikia nepamiršti, kad z testas naudojamas tik tada, kai imties dydis yra didesnis nei 30, priešingu atveju naudojamas t testas.

seychellesartprojects.org