Portfelio grąžinimo formulė Apskaičiuokite viso portfelio grąžą Pavyzdys
Viso portfelio grąžos apskaičiavimo formulė
Portfelio grąžos formulė naudojama apskaičiuojant viso portfelio, susidedančio iš skirtingų atskirų aktyvų, grąžą, kur pagal formulę portfelio grąža apskaičiuojama apskaičiuojant individualaus turto uždirbtų investicijų grąžą, padaugintą iš jų atitinkamos svorio klasės viso portfelio sudedant visus gautus rezultatus.
Portfelio grąža gali būti apibrėžiama kaip investicijų grąžos, uždirbtos už atskirą turtą, produkto su viso to portfelio svorio klase suma. Tai reiškia portfelio grąžą, o ne atskirą turtą.
Tikėtiną grąžą galima apskaičiuoti pagal galimų rezultatų (t. Y. Grąžos, kurią žemiau reiškia r), pagal kiekvieno portfelio turto svorį (t. Y. Su w) sandaugą ir po to apskaičiuojant tų rezultatų sumą.
R p = ∑n i = 1 w i r i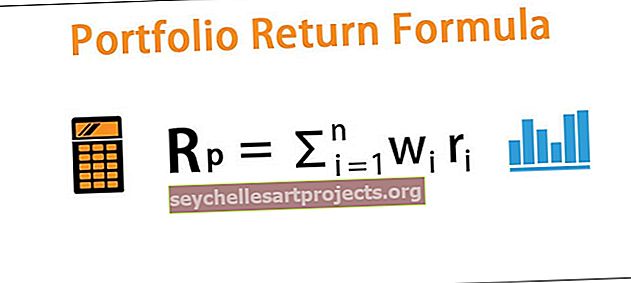
Kur ∑n i = 1 w i = 1
- w yra kiekvieno turto svoris
- r yra turto grąža
Portfelio grąžos apskaičiavimas (žingsnis po žingsnio)
Portfelio grąžos apskaičiavimas yra gana paprastas, tačiau tam reikia skirti mažai dėmesio.
- 1 žingsnis: Gaukite individualią turto grąžą, į kurią buvo investuotos lėšos. Pvz., Jei investuotojas investavo į nuosavą kapitalą, reikia apskaičiuoti visą grąžą, ty bendrą grąžą, įskaitant tarpinius pinigų srautus, kurie akcijų atveju būtų dividendai.
- 2 žingsnis: Apskaičiuokite atskiro turto, į kurį investuojamos lėšos, svorį. Tai galima padaryti padalijus to turto investuotą sumą iš viso investuoto fondo.
- 3 žingsnis: Paimkite grąžinimo sandaugą, apskaičiuotą 1 žingsnyje, su svoriu, apskaičiuotu 2 žingsnyje.
- 4 žingsnis: trečias žingsnis bus kartojamas, kol bus baigti viso turto skaičiavimai. Pagaliau turime susumuoti visų atskirų turto grąžų sandaugą pagal svorio kategoriją, kuri bus portfelio grąža.
Pavyzdžiai
Šį „Portfolio Return Formula Excel“ šabloną galite atsisiųsti čia - „Portfolio Return Formula Excel“ šablonas1 pavyzdys
Apsvarstykite, ar „ABC ltd“ turto valdymo įmonė investavo į 2 skirtingus turtus kartu su praėjusiais metais uždirbta grąža. Jūs turite uždirbti portfelio grąžą.

Sprendimas:
Mums suteikiama individuali turto grąža ir investicijų suma, todėl pirmiausia sužinosime svorius taip:

- Svoris (1 turto klasė) = 1 000 000,00 / 1 500 000,00 = 0,67
Panašiai apskaičiavome 2 turto klasės svorį

- Svoris (1 turto klasė) = 50 000,00 / 1 500 000,00 = 0,33
Dabar, norėdami apskaičiuoti portfelio grąžą, turime padauginti svorius su turto grąža ir tada mes susumuosime tas pajamas.

- W i R I (aktyvų 1-os klasės) = 0,67 * 10% = 6,67%
panašiai, mes apskaičiuojamas W i R i Asset klasės 2
- W i R I (aktyvų klasė 2) = 0,33 * 11%
- = 3,67%
Portfelio grąža apskaičiuojama taip,

Portfelio grąža

Portfelio grąža bus 10,33%
2 pavyzdys
„JP Morgan“ vijosi vieną didžiausių investicinės bankininkystės firmų, keletą kartų investavo į įvairias turto klases. Ponas Dimonas, bendrovės pirmininkas, yra suinteresuotas žinoti visų įmonės investicijų grąžą. Jūs turite apskaičiuoti portfelio grąžą.

Sprendimas:
Mums čia suteikiama tik naujausia rinkos vertė ir tiesiogiai grąžos nėra. Taigi pirmiausia turime apskaičiuoti atskiro turto grąžą.
Turime atimti investicijos sumą iš rinkos vertės, kad gautume perteklinę grąžą, o paskui tą patį padaliję iš investicijų sumos gausime grąžą iš atskiro turto.

Pastaba: Išsamų skaičiavimą žr. „Excel“ šablone
Dabar mes turime atskirą turto grąžą ir kartu su ta investicijų suma, o dabar mes sužinosime svorius naudodami investicijų sumą, o ne rinkos vertę taip,

Akcijų svoris = 300000000/335600000 = 0,3966
Panašiai apskaičiavome visų kitų duomenų svorį.

Dabar, norėdami apskaičiuoti portfelio grąžą, turime padauginti svorius su turto grąža ir tada mes susumuosime tas pajamas.

Portfelio grąža apskaičiuojama taip,

Portfelio grąža

Taigi „JP Morgan“ uždirbta portfelio grąža yra 21,57%
3 pavyzdys
Gautamas yra asmuo, neseniai pradėjęs investuoti į rinką. Jis investavo į XYZ akcijas už 100 000, o tai praėjo metus. Nuo tada jis gavo 5000 dividendų, o dabartinė XYZ akcijų rinkos vertė prekiauja 10% priemoka. Be to, jis investavo į fiksuotą indėlį už 20 000, o bankas teikia 7% grąžą. Galiausiai, jis investavo į žemę savo gimtajame mieste už 500 000, o dabartinė rinkos vertė yra 700 000. Jis kreipėsi į jus, kad apskaičiuotų portfelio grąžą.

Sprendimas:
Mums čia suteikiama tik naujausia rinkos vertė ir tiesiogiai grąžos nėra. Taigi pirmiausia turime apskaičiuoti atskiro turto grąžą.
Turime atimti investicijos sumą iš rinkos vertės, kad gautume perteklinę grąžą, o paskui tą patį padaliję iš investicijų sumos gausime grąžą iš atskiro turto.

Pastaba: Išsamios skaičiavimo informacijos ieškokite „Excel“ šablone.
Dabar mes turime atskirą turto grąžą ir kartu su ta investicijų suma, o dabar mes sužinosime svorius naudodami investicijos sumą, o ne rinkos vertę.

- Svoris (XYZ atsargos) = 1,00,000 / 6,20,000 = 0,1613
Panašiai apskaičiavome ir kitų duomenų svorį.
Dabar, norėdami apskaičiuoti portfelio grąžą, turime padauginti svorius su turto grąža ir tada mes susumuosime tas pajamas.

(XYZ atsargos) W i R i = 0,15 * 0,1613 = 2,42%
Panašiai apskaičiavome W i Ri ir kitiems.
Portfelio grąža apskaičiuojama taip,

Portfelio grąža

Taigi p. Gautamo uždirbta portfelio grąža yra 35,00%
Aktualumas ir naudojimas
Labai svarbu suprasti portfelio tikėtinos grąžos formulės sampratą, nes tą patį naudos ir tie investuotojai, kad jie galėtų numatyti pelną ar nuostolius, kurie gali atsirasti dėl jų investuotų fondų. Remdamasis šia tikėtinos grąžos formule, investuotojas gali priimti sprendimą investuoti į turtą, atsižvelgdamas į jų tikėtiną grąžą.
Be to, investuotojas taip pat galės nuspręsti dėl turto svorio portfelyje, ty kokia lėšų dalis turėtų būti investuota, ir tada atlikti reikiamą pakeitimą.
Be to, investuotojas gali naudoti tikėtinos grąžos formulę reitinguodamas atskirą turtą ir toliau investuoti lėšas pagal reitingą ir galiausiai įtraukti juos į savo portfelį. Kitaip tariant, jis padidintų tos turto klasės, kurios laukiama grąža yra didesnė, svorį.