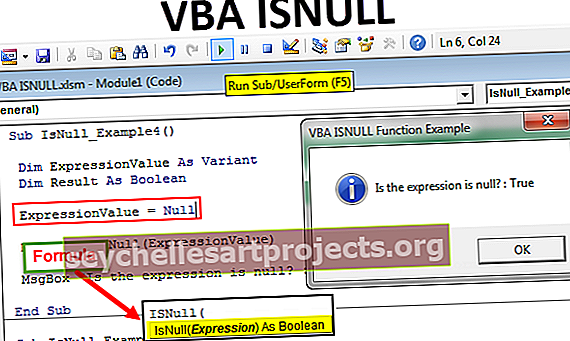
Standartinio nuokrypio formulė Žingsnis po žingsnio skaičiavimas
Kas yra standartinio nuokrypio formulė?
Standartinis nuokrypis (SD) yra populiarus statistikos įrankis, kurį žymi graikų raidė „σ“ ir kuris naudojamas matuoti duomenų verčių rinkinio kitimo ar dispersijos dydį, palyginti su jo vidurkiu (vidurkiu), taip interpretuojant duomenys. Jei jis yra mažesnis, duomenų taškai yra arti vidutinės vertės, taigi rodo patikimumą. Bet jei jis didesnis, duomenų taškai skiriasi nuo vidurkio.
Standartinio nuokrypio formulė pateikta žemiau


Kur:
- xi = kiekvieno duomenų taško vertė
- x̄ = Vidurkis
- N = duomenų taškų skaičius
- Standartinis nuokrypis yra plačiausiai naudojamas ir praktikuojamas portfelio valdymo paslaugose, o fondų valdytojai dažnai naudoja šį pagrindinį metodą apskaičiuodami ir pateisindami savo grąžas tam tikrame portfelyje.
- Aukštas standartinis portfelio nuokrypis reiškia, kad tam tikrame portfelyje yra didelis tam tikro akcijų skaičiaus skirtumas, o, kita vertus, mažas standartinis nuokrypis reiškia mažesnį akcijų skirtumą.
- Rizikos nenorintis investuotojas bus pasirengęs prisiimti bet kokią papildomą riziką tik tuo atveju, jei jam ar jai kompensuojama lygi ar didesnė grąžos suma, kad galėtų prisiimti tą konkrečią riziką.
- Labiau rizikuojantis investuotojas gali būti nepatenkintas savo standartiniu nuokrypiu ir norėtų į saugesnį investavimą įtraukti tokias vyriausybės obligacijas ar didelių kapitalizacijų akcijas į savo portfelį ar investicinius fondus, kad diversifikuotų portfelio ir jo riziką standartinis nuokrypis ir dispersija.
- Dispersija ir glaudžiai susijęs standartinis nuokrypis yra tai, kaip pasiskirstymas pasiskirsto. Kitaip tariant, tai yra kintamumo matai.
Standartinio nuokrypio apskaičiavimo žingsniai
- 1 žingsnis: Pirma, stebėjimų vidurkis apskaičiuojamas taip pat, kaip ir vidurkis, pridedant visus duomenų rinkinyje esančius duomenų taškus ir padalijant iš stebėjimų skaičiaus.
- 2 žingsnis: Tada kiekvieno duomenų taško dispersija matuojama vidurkiu, kuris gali būti teigiamas arba neigiamas skaičius, tada vertė yra kvadratas, o rezultatas atimamas iš vieno.
- 3 žingsnis: Tada dispersijos kvadratas, apskaičiuotas pagal 2 žingsnį, imamas standartiniam nuokrypiui apskaičiuoti.
Pavyzdžiai
Šį standartinio nuokrypio formulės „Excel“ šabloną galite atsisiųsti čia - standartinio nuokrypio formulės „Excel“ šabloną1 pavyzdys
Duomenų taškai pateikti 1,2 ir 3. Koks yra pateikto duomenų rinkinio standartinis nuokrypis?
Sprendimas:
Norėdami apskaičiuoti standartinį nuokrypį, naudokite šiuos duomenis

Taigi, dispersijos apskaičiavimas bus -

Dispersija = 0,67
Standartinio nuokrypio apskaičiavimas bus:

Standartinis nuokrypis = 0,82
2 pavyzdys
Raskite standartinį nuokrypį 4,9,11,12,17,5,8,12,14.
Sprendimas:
Norėdami apskaičiuoti standartinį nuokrypį, naudokite šiuos duomenis

Vidurkio apskaičiavimas bus -

Pirmiausia raskite duomenų taško 4 + 9 + 11 + 12 + 17 + 5 + 8 + 12 + 14/9 vidurkį
Vidurkis = 10,22
Taigi, dispersijos apskaičiavimas bus -

Dispersija bus -

Dispersija = 15,51
Standartinio nuokrypio apskaičiavimas bus:

Standartinis nuokrypis = 3,94
Dispersija = standartinio nuokrypio kvadratinė šaknis
3 pavyzdys
Norėdami apskaičiuoti standartinį nuokrypį, naudokite šiuos duomenis

Taigi, dispersijos apskaičiavimas bus -

Dispersija = 132,20
Standartinio nuokrypio apskaičiavimas bus:

Standartinis nuokrypis = 11,50
Tokio tipo skaičiavimus portfelio valdytojai dažnai naudoja apskaičiuodami portfelio riziką ir grąžą.
Aktualumas ir naudojimas
- Standartinis nuokrypis yra naudingas analizuojant bendrą riziką ir grąžinant portfelio matricą ir istoriškai naudingas, jis yra plačiai naudojamas ir praktikuojamas pramonėje. Standartinis portfelio nuokrypis gali būti paveiktas koreliacijos ir portfelio akcijų svorio. .
- Kadangi dviejų portfelio turto klasių koreliacija sumažina portfelio riziką, apskritai sumažėja, tačiau nebūtina visą laiką, kad vienodai įvertintas portfelis sukurtų mažiausiai rizikos visatoje.
- Didelis standartinis nuokrypis gali būti nepastovumo matas, tačiau tai nebūtinai reiškia, kad toks fondas yra blogesnis nei tas, kurio standartinis nuokrypis yra mažas. Jei pirmasis fondas yra daug geresnis nei antrasis, nukrypimas nebus svarbus.
- Standartinis nuokrypis taip pat naudojamas statistikoje, jį dėsto profesoriai tarp įvairių geriausių pasaulio universitetų, tačiau standartinio nuokrypio formulė keičiama, kai ji naudojama imties nuokrypiui apskaičiuoti.
- SD lygtis pavyzdyje = tik vardiklis sumažinamas 1