seychellesartprojects.org

Efektyvios palūkanų normos apibrėžimas

Efektyvi palūkanų norma, dar vadinama metine ekvivalentine palūkanų norma, yra palūkanų norma, kurią asmuo faktiškai moka arba uždirba už finansinę priemonę, kuri apskaičiuojama atsižvelgiant į padidėjusio laikotarpio poveikį.

Efektyvi palūkanų normos formulė

Efektyvios palūkanų normos formulė = (1 + i / n) n -

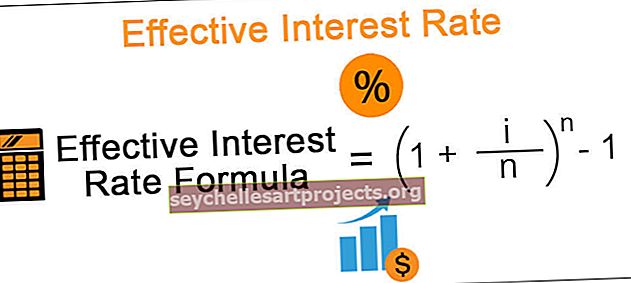
Čia i = metinė palūkanų norma, paminėta priemonėje.

n = Tai sudaro sudėtinių laikotarpių skaičių per metus.

Interpretacijos

Sudėjus keičiasi palūkanų norma. Štai kodėl instrumento palūkanų norma nėra efektyvi palūkanų norma (metinė ekvivalentinė norma) investuotojui. Pvz., Jei priemonei parašyta 11% palūkanų norma ir palūkanų norma padidinama keturis kartus per metus, metinė ekvivalentinė norma negali būti 11%.

Kas tada būtų?

Tai būtų - (1 + i / n) n - 1 = (1 + 0,11 / 4) 4 - 1 = 1.1123 - 1 = 0.1123 = 11.23%.

Tai reiškia, kad 11,23% būtų faktinė investuotojo palūkanų norma.

Net jei pakeitimas yra menkas, jis nėra tas pats, kas metinė palūkanų norma, minima priemonėje.

Pavyzdys

1 pavyzdys

Tingas nusipirko tam tikrą instrumentą. Minėta priemonės palūkanų norma yra 16%. Jis investavo apie 100 000 USD. Instrumentas jungiasi kasmet. Kokia būtų faktinė palūkanų norma (AER) šiai konkrečiai priemonei? Kiek jis kasmet gautų kaip palūkanas?

Efektyvi palūkanų norma ir metinė palūkanų norma ne visada būna vienodos, nes palūkanos kasmet padidėja kelis kartus. Kartais palūkanų norma padidinama kas pusmetį, ketvirtį ar mėnesį. Tuo metinė ekvivalentinė norma skiriasi nuo metinės palūkanų normos.

Šis pavyzdys jums tai parodo.

Paskaičiuokime.

Kadangi palūkanų norma didinama kasmet, tai būtų efektyvios palūkanų normos formulė -

(1 + i / n) n - 1 = (1 + 0,16 / 1) 1 - 1 = 1,16 - 1 = 0,16 = 16%.

Tai reiškia, kad šiame konkrečiame pavyzdyje nebūtų skirtumo tarp metinės palūkanų normos ir metinės ekvivalentinės normos (AER).

Kiekvienais metais Tingas gautų palūkanas už = (100 000 USD * 16%) = 16 000 USD už instrumentą.

2 pavyzdys

Tongas nusipirko tam tikrą instrumentą. Minėta priemonės palūkanų norma yra 16%. Jis investavo apie 100 000 USD. Instrumentas jungiasi šešis kartus per metus. Kokia būtų šios konkrečios priemonės metinė ekvivalentinė norma (AER)? Kiek jis kasmet gautų kaip palūkanas?

Tai tik ankstesnio pavyzdžio pratęsimas.

Tačiau yra didžiulis skirtumas.

Ankstesniame pavyzdyje priemonė buvo padidinta kartą per metus, todėl metinė palūkanų norma buvo panaši į metinę lygiavertę palūkanų normą.

Tačiau šiuo atveju scenarijus yra visiškai kitoks.

Čia turime palūkanų normą, kuri padidinama šešis kartus per metus.

Taigi, čia yra metinės palūkanų normos formulė -

(1 + i / n) n - 1 = (1 + 0,16 / 6) 6 - 1 = 1,171 - 1 = 0,171 = 17,1%.

Dabar matote, kad jei palūkanų norma padidinama šešis kartus per metus, metinė ekvivalentinė norma tampa visiškai kitokia.

Dabar, kai turime efektyvią palūkanų normą, galime apskaičiuoti palūkanas, kurias Tongas gaus metų pabaigoje.

Tongas gaus = (100 000 USD * 17,1%) = 17 100 USD.

Jei palyginsime palūkanas, kurias Ting gauna ankstesniame pavyzdyje, su „Tong“, nes palūkanų normos susidaro skirtingai, pamatysime, kad palūkanos skiriasi maždaug 1100 USD.

3 pavyzdys

Pingas investavo į instrumentą. Ji investavo 10 000 USD. Instrumente minima palūkanų norma yra 18%. Palūkanos padidinamos kas mėnesį. Sužinokite, kaip pirmaisiais metais Ping gaus palūkanas kiekvieną mėnesį.

Tai yra labai išsamus metinės ekvivalentinės normos pavyzdys.

Šiame pavyzdyje parodysime, kaip iš tikrųjų vyksta skaičiavimas, nenaudojant efektyvios palūkanų normos formulės.

Pažiūrėkime.

Kadangi palūkanų norma didinama kas mėnesį, faktinis minėtos palūkanų normos pasiskirstymas per mėnesį yra = (18/12) = 1,5%.

• Pirmąjį mėnesį „Ping“ gaus palūkanas = (10 000 * 1,5%) = 150 USD.
• Antrą mėnesį „Ping“ gaus palūkanas = {(10 000 + 150) * 1,5%} = (10 150 * 1,5%) = 152,25 USD.
• Trečią mėnesį „Ping“ gaus palūkanas = {(10 000 + 150 + 152,25) * 1,5%} = (10 302,25 * 1,5%) = 154,53 USD.
• Ketvirtą mėnesį „Ping“ gaus palūkanas = {(10 000 + 150 + 152,25 + 154,53) * 1,5%} = (10 456,78 * 1,5%) = 156,85 USD.
• Penktą mėnesį „Ping“ gaus palūkanas = {(10 000 + 150 + 152,25 + 154,53 + 156,85) * 1,5%} = (10 613,63 * 1,5%) = 159,20 USD.
• Šeštą mėnesį „Ping“ gaus palūkanas = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20) * 1,5%} = (10 772,83 * 1,5%) = 161,59 USD.
• Septintą mėnesį „Ping“ gaus palūkanas = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59) * 1,5%} = (10 934,42 * 1,5%) = 164,02 USD.
• Aštuntą mėnesį „Ping“ gaus palūkanas = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02) * 1,5%} = (11098,44 * 1,5%) = 166,48 USD.
• Devintą mėnesį „Ping“ gaus palūkanas = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48) * 1,5%} = (11264,92 * 1,5%) = 168,97 USD.
• Dešimtą mėnesį „Ping“ gaus palūkanas = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48 + 168,97) * 1,5%} = (11433,89 * 1,5%) = 171,51 USD.
• Vienuoliktą mėnesį Pingas gaus palūkanas = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48 + 168,97 + 171,51) * 1,5%} = (11605,40 * 1,5%) = 174,09 USD.
• Dvyliktą mėnesį „Ping“ gaus palūkanas = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48 + 168,97 + 171,51 + 174,09) * 1,5%} = (11779,49 * 1,5%) = 176,69 USD.

Bendras Pingo susidomėjimas šiais metais yra -

• (150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48 + 168,97 + 171,51 + 174,09 + 176,69) = 1956,18 USD.

• Metinė ekvivalento normos formulė = (1 + i / n) n - 1 = (1 + 0,18 / 12) 12 - 1 = 1,195618 - 1 = 0,195188 = 19,5618%.

Taigi, palūkanos, kurias gaus Ping = (10 000 USD ^ 19,5618%) = 1956,18 USD.

Efektyvi palūkanų norma „Excel“

Norint rasti efektyvią palūkanų normą ar metinę ekvivalentinę normą „Excel“, mes naudojame „Excel“ funkciją EFFECT.

• nominal_rate yra palūkanų norma
• nper - sudedamųjų laikotarpių skaičius per metus

Pažiūrėkime žemiau pateiktą pavyzdį

• Jei jūsų nominali palūkanų norma yra 10% per metus, metinė ekvivalentinė norma yra tokia pati kaip 10%.
• Jei jūsų nominali palūkanų norma yra 10% kartu su šešiais mėnesiais, metinė ekvivalento norma yra tokia pati kaip 10,25%.
• Jei jūsų nominali palūkanų norma yra 10%, susidedanti kas ketvirtį, metinė ekvivalento norma yra tokia pati kaip 10,38%.
• Jei jūsų nominali palūkanų norma yra 10% per mėnesį, metinė ekvivalento norma yra tokia pati kaip 10,47%.
• Jei jūsų nominali palūkanų norma yra 10% per dieną, faktinė palūkanų norma yra tokia pati kaip 10,52%.

Siūlomi skaitymai

Tai buvo efektyvios palūkanų normos ir jos apibrėžimo vadovas. Čia aptariame efektyvios palūkanų normos formulę ir žingsnis po žingsnio skaičiavimus. Norėdami sužinoti daugiau, skaitykite šiuos straipsnius

• Neigiamos palūkanų normos pavyzdys
• Apskaičiuokite dalyvavimo rodiklį
• Skirtumai - diskonto norma ir palūkanų norma
• Nominali palūkanų normos formulė
• Cointegration
<