seychellesartprojects.org

Formulė vidurkiui apskaičiuoti

Vidurkis yra reikšmė, naudojama duomenų reikšmių rinkiniui reprezentuoti, kaip ir vidurkis, apskaičiuotas pagal visus duomenis, ir ši formulė apskaičiuojama sudedant visas pateikto rinkinio vertes, žymimas susumuojant X, ir padalijant ją iš duomenų skaičiaus. reikšmės pateiktos rinkinyje, pažymėtame N.

Vidutinis = (a ₁ + a ₂ +…. + A _n ) / n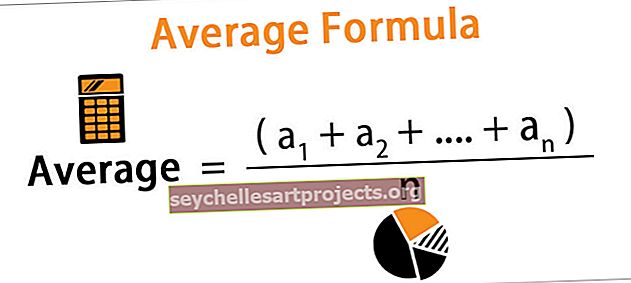

• kur a _i = i stebėjimas
• n = stebėjimų skaičius

Paaiškinimas

Vidutinį apskaičiavimą galima apskaičiuoti atlikus šiuos veiksmus:

• 1 žingsnis: Pirma, nustatykite stebėjimą ir jie žymimi ₁ , ₂ , ... .., a _n, atitinkančiu 1-ąjį, 2-ąjį, ..., n-tą stebėjimą.
• 2 žingsnis: Tada nustatykite stebėjimų skaičių ir jis žymimas n.
• 3 žingsnis: Galiausiai, vidurkis apskaičiuojamas sudėjus visus stebėjimus, o rezultatą padalijant iš stebėjimų skaičiaus, kaip parodyta žemiau.

Vidutinis = (a ₁ + a ₂ +…. + A _n ) / n

Pavyzdžiai

Šį „Average Formula Excel“ šabloną galite atsisiųsti čia - „Average Formula Excel“ šablonas

1 pavyzdys

Paimkime Jono, įstojusio į aplinkos mokslų studijų programą, pavyzdį. Trejų metų studijų kursas yra padalintas į šešis semestrus, o galutinis vidutinis procentas apskaičiuojamas pagal procentus, surinktus per visus semestrus. Apskaičiuokite galutinį Jono procentą pagal šį jo balą:

Žemiau pateikiami duomenys, skirti apskaičiuoti vidutinį procentą.

Atsižvelgiant į tai,

a ₁ = 79%, a ₂ = 81%, a ₃ = 74%, a ₄ = 70%, a ₅ = 82%, a ₆ = 85%, n = 6

Naudojant aukščiau pateiktą informaciją, vidurkis bus apskaičiuojamas taip,

•   Vidutinis = (79% + 81% + 74% + 70% + 82% + 85%) / 6

Vidutinis bus -

• Vidutinis = 78,50%

Todėl Davidas baigimo programoje surinko galutinį 78,5% procentą.

Naudoja

Kaip rodo pavadinimas „vidutinis“, jis nurodo centrinį stebėjimo taško tašką ir, kai jis naudojamas matematikos srityje, jis reiškia skaičių, kuris paprastai reiškia skaičių grupės vidurkį. Šis terminas dažnai vartojamas išreikšti skaičių, kuris reiškia žmonių ar daiktų grupę. Tai labai svarbu, nes tai padeda apibendrinti didelį duomenų kiekį į vieną vertę ir taip pat rodo, kad pirminiuose duomenyse esama tam tikros nenuoseklumo apie vieną vertę, kuri yra labai svarbi centrinės tendencijos teorijos dalis.