seychellesartprojects.org

Formulė apskaičiuoti Sharpe santykį

Investuotojai naudoja „Sharpe“ santykio formulę, kad apskaičiuotų perteklinę grąžą, palyginti su nerizikinga grąža, už portfelio nepastovumo vienetą ir pagal formulę nerizikinga grąžos norma atimama iš laukiamos portfelio grąžos ir rezultatas dalijamas iš portfelio standartinio nuokrypio.

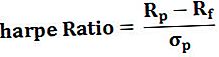
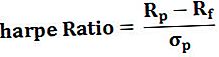
Kur,

• R _p = portfelio grąža
• R _f  = nerizikinga norma
• σp = portfelio perteklinės grąžos standartinis nuokrypis.

Kaip apskaičiuoti Sharpe santykį?

• „Sharpe“ santykis apskaičiuojamas dalijant portfelio grąžos ir nerizikingos normos skirtumą iš portfelio perteklinės grąžos standartinio nuokrypio. Tai mes galime įvertinti investicijų rezultatus remdamiesi nerizikinga grąža.
• Aukštesnė Sharpe metrika visada yra geresnė nei žemesnė, nes didesnis santykis rodo, kad portfelis priima geresnį sprendimą investuoti.
• „Sharpe“ santykis taip pat padeda paaiškinti, ar perteklinė portfelio grąža yra dėl gero investavimo sprendimo, ar dėl per didelės rizikos. Kuo didesnė rizika, tuo didesnė grąža, tuo mažesnė rizika mažina grąžą.
• Jei vieno iš portfelių grąža yra didesnė nei konkurentų, tai yra gera investicija, nes grąža yra didelė ir rizika yra ta pati. Tai apie maksimalią grąžą ir nepastovumo mažinimą. Jei kurios nors investicijos grąža yra 15%, o nepastovumas yra lygus nuliui. Tada Sharpe santykis bus begalinis. Didėjant nepastovumui, rizika žymiai padidėja, nes padidėja ir grąžos norma.

Pažiūrėkime, koks yra „Sharpe“ santykio vertinimo slenkstis.

1. <1 - nėra gerai
2. 1-1,99 - Gerai
3. 2–2,99 - tikrai gerai
4. > 3 - išskirtinis

Neribotos rizikos portfelis, kaip tik iždo vekselis, kadangi investicija yra nerizikinga, nėra nepastovumo ir uždarbio, viršijančio nerizikingą normą. Taigi „Sharpe“ santykis neturi nulinio portfelio.

• 1, 2, 3 metrikoje yra didelis rizikos laipsnis. Jei metrika yra didesnė arba lygi 3, tai laikoma puikiu „Sharpe“ matavimu ir gera investicija.
• Kadangi metrika yra didesnė arba lygi 1 ir 2 mažesnė nei 2, laikoma, kad tai tik gerai, o jei metrika yra didesnė arba lygi 2 ir mažesnė nei 3, manoma, kad ji tikrai gera.
• Jei metrika yra mažesnė nei 1, ji nelaikoma gera.

Pavyzdžiai

Šį „Sharpe Ratio Formula Excel“ šabloną galite atsisiųsti čia - „Sharpe Ratio Formula Excel“ šablonas

1 pavyzdys

Tarkime, yra du investiciniai fondai, kuriuos galima palyginti su skirtingais portfeliais, turinčiais skirtingą rizikos lygį. Dabar pažiūrėkime apie „Sharpe“ santykį, kad sužinotume, kuris iš jų veikia geriau.

Vidutinio kapitalo akcijų fondo investicijos ir išsami informacija yra tokia: -

• Portfelio grąža = 35%
• Nerizikinga norma = 15%
• Standartinis nuokrypis = 15

Taigi Sharpe santykis bus apskaičiuojamas taip:

• Sharpe santykio lygtis = (35-10) / 15
• Sharpe santykis = 1,33

„Bluechip Fund“ investicijos ir išsami informacija yra tokia: -

• Portfelio grąža = 30%
• Nerizikinga norma = 10%
• Standartinis nuokrypis = 5

Taigi Sharpe santykis bus apskaičiuojamas taip:

• Sharpe santykis = (30–10) / 5
• Sharpe santykis = 4

Todėl aukščiau minėto investicinio fondo „Sharpe“ santykiai yra tokie,

• „Bluechip“ fondas = 4
• Vidutinio kapitalo fondas = 1,33

„Bluechip“ investicinis fondas pralenkė „Mid cap“ investicinį fondą, tačiau tai nereiškia, kad „Mid cap“ investicinis fondas pasirodė gerai, palyginti su jo rizikos lygiu. Šarpe papasakok mums žemiau: -

• „Blue-chip“ investicinis fondas pasirodė geriau nei „Mid cap“ savitarpio investicinis fondas, palyginti su investicijos rizika.
• Jei vidutinio kapitalo investicinis fondas veiktų taip pat gerai, kaip ir „Bluechip“ investicinis fondas, palyginti su rizika, jis gautų didesnę grąžą.
• Šiais metais „bluechip“ investicinis fondas uždirbo didesnę grąžą, tačiau rizika yra didelė. Taigi ateityje jis bus nepastovus.

2 pavyzdys

Čia vienas investuotojas laiko 5 000 000 USD investuotą portfelį, kurio laukiama grąžos norma yra 12%, o kintamumas - 10%. Veiksmingas portfelis tikisi grąžos, viršijančios 17%, ir 12% nepastovumo. Nerizikinga palūkanų norma yra 4%. „Sharpe“ santykį galima apskaičiuoti taip:

• Sharpe santykis = (0,12 - 0,04) / 0,10
• Sharpe santykis = 0,80

„Sharpe Ratio“ skaičiuoklė

Galite naudoti šią „Sharpe Ratio“ skaičiuoklę.

Portfelio grąžinimas
Nerizikinga norma
Standartinis portfelio grąžos perviršis
Aštrių santykių formulė =

Aštrių santykių formulė =

Portfelio grąža - nerizikinga norma = Standartinis portfelio grąžos perviršis

0 - 0 = 0 0

Privalumai

Šarpo santykio pranašumai yra šie:

• Šis santykis yra vidutinė uždirbta grąža, viršijanti nerizikingą normą, tenkančią vieneto nepastovumui arba visai rizikai
• Sharpe santykis padeda palyginti investicijas.
• Šarpo santykis padeda palyginti rizikos ir grąžos santykius.

Naudojant „Sharpe“ santykį yra keletas klausimų, kurie apskaičiuojami darant prielaidą, kad investicijų grąža paprastai paskirstoma ir dėl to atitinkami „Sharpe“ santykio aiškinimai yra klaidingi.

„Sharpe Ratio“ skaičiavimas programoje „Excel“

Žemiau pateiktame šablone pateikiami vidutinio kapitalo investicinių fondų ir „Bluechip“ investicinių fondų duomenys, skirti apskaičiuoti „Sharpe“ santykį.

Žemiau pateiktame „Excel“ šablone mes naudojome „Sharpe“ santykio lygties apskaičiavimą, kad rastume „Sharpe“ santykį.

Taigi Sharpe santykio apskaičiavimas bus