seychellesartprojects.org

Kas yra harmoninė reikšmė?

Harmoninis vidurkis yra abipusis aritmetinio vidurkio vidurkis, ty vidurkis apskaičiuojamas dalijant nurodyto duomenų rinkinio stebėjimų skaičių iš jo abipusės sumos (1 / Xi) kiekviename nurodytame duomenų rinkinyje.

Vidutinė harmoninė formulė

Harmoninis vidurkis = n / ∑ [1 / X _i ]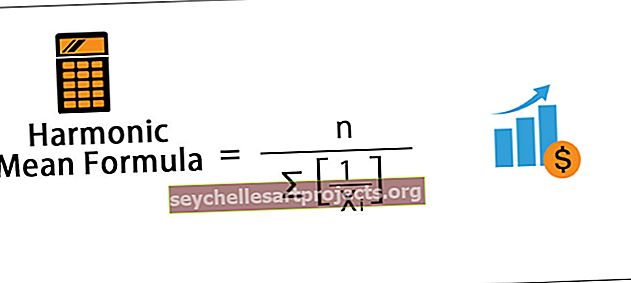

• Galima pastebėti, kad tai yra normalaus vidurkio abipusis skaičius.
• Harmoninis vidutinio vidurkio vidurkis yra ∑ x / n, taigi, jei formulė yra atvirkštinė, ji tampa n / ∑x, tada visos vardiklio reikšmės, kurias reikia naudoti, turėtų būti abipusės, ty skaitikliui ji lieka „n“, bet vardiklis vertes ar jų stebėjimus, kuriuos turime naudoti abipusėms vertėms.
• Išvestinė vertė visada būtų mažesnė nei vidutinė arba pasakys aritmetinį vidurkį.

Pavyzdžiai

Šį „Harmonic Mean Formula Excel“ šabloną galite atsisiųsti iš čia - „Harmonic Mean Formula Excel“ šablonas

1 pavyzdys

Apsvarstykite šių skaičių duomenų rinkinį: 10, 2, 4, 7. Naudodami aukščiau aptartą formulę, turite apskaičiuoti harmoninį vidurkį.

Sprendimas:

Skaičiavimui naudokite šiuos duomenis.

Harmoninis vidurkis = n / ∑ [1 / X _i ]

= 4 / (1/10 + 1/2 + 1/4 + 1/7)

= 4 / 0,99

2 pavyzdys

Ponas Vijay yra „JP Morgan“ akcijų analitikas. Jo vadybininkas paprašė jo nustatyti indekso P / E santykį, kuris rodo bendrovės W, X ir Y akcijų kainas. Įmonė W praneša apie 40 milijonų dolerių uždarbį ir 2 milijardų dolerių rinkos kapitalizaciją, praneša bendrovė X 3 mlrd. USD, o rinkos kapitalizacija - 9 mlrd. USD, o „Y“ įmonė praneša apie 10 mlrd. USD uždarbį ir 40 mlrd. Apskaičiuokite indekso P / E santykio harmoninį vidurkį.

Sprendimas:

Skaičiavimui naudokite šiuos duomenis

Pirmiausia apskaičiuosime P / E santykį

P / E santykis iš esmės yra (rinkos kapitalizacija / pajamos).

• (Įmonės W) P / E = (2 mlrd. USD) / (40 mln. USD) = 50
• (Įmonės X) P / E = (9 mlrd. USD) / (3 mlrd. USD) = 3
• (Įmonės Y) P / E = (40 mlrd. USD) / (10 mlrd. USD) = 4

1 / X vertės apskaičiavimas

• Bendrovė W = 1/50 = 0,02
• X įmonė = 1/3 = 0,33
• Įmonė Y = 1/4 = 0,25

Skaičiavimą galima atlikti taip,

Harmoninis vidurkis = n / ∑ [1 / X _i ]

• = 3 / (1/50 + 1/3 + 1/4)
• = 3 / 0,60

3 pavyzdys

Rey, šiaurinės Kalifornijos gyventojas, yra profesionalus sportinis baikeris ir sekmadienio vakarą apie 17:00 EST vyksta į savo turą po paplūdimį iš savo namų. Pirmąją kelionės pusę jis važiuoja 50 mylių per valandą greičiu, o antrąją pusę - 70 mylių per valandą greičiu nuo savo namų iki paplūdimio. Koks bus jo vidutinis greitis?

Sprendimas:

Skaičiavimui naudokite šiuos duomenis.

Šiame pavyzdyje Rey išvyko į kelionę tam tikru greičiu, o čia vidurkis bus pagrįstas atstumu.

Skaičiavimą galima atlikti taip,

Čia mes galime apskaičiuoti vidutinį Rey sportinio dviračio greičio harmoninį vidurkį.

Harmoninis vidurkis = n / ∑ [1 / X _i ]

• = 2 / (1/50 + 1/70)
• = 2 / 0,03

Rey sportinio dviračio vidutinis greitis yra 58,33.

Naudojimas ir aktualumas

Harmoninės priemonės, kaip ir kitos vidutinės formulės, taip pat yra kelios, ir jos dažniausiai naudojamos finansų srityje tam tikriems duomenims, pvz., Kainų kartotiniams, apskaičiuoti. Finansinių daugiklių, tokių kaip P / E santykis, negalima skaičiuoti naudojant įprastą vidurkį ar aritmetinį vidurkį, nes šie vidurkiai yra nukreipti į didesnes vertes. Be to, darnios harmonijos priemonės gali būti naudojamos tam tikro tipo modeliams, pvz., „Fibonači“ sekoms, kurios dažniausiai naudojamos, nustatyti rinkos technikų atliekamoje techninėje analizėje.

Harmoninis vidurkis taip pat apima vienetų, tokių kaip greičiai, santykiai ar greitis, ir tt vidurkius. Be to, svarbu pažymėti, kad tam įtakos turi kraštutinės vertės nurodytame duomenų rinkinyje arba tam tikrame stebėjimų rinkinyje.

Harmoninis vidurkis yra apibrėžtas griežtai ir yra pagrįstas visomis tam tikro duomenų rinkinio ar imties vertėmis arba visais stebėjimais ir gali būti tinkamas tolesniam matematiniam gydymui. Kaip ir geometrinis vidurkis, harmoninis vidurkis taip pat neturi didelės įtakos stebėjimų ar imčių svyravimams. Tai teiktų didesnę reikšmę mažoms vertybėms ar mažiems stebėjimams, ir tai bus naudinga tik tada, kai toms mažoms vertybėms ar toms mažoms pastaboms reikės skirti didesnį svorį.